The overshoot in the stress at time t=1.0 is due in part to the instantaneous change from a surface load increasing at constant rate to a constant surface load.  This effect can be minimized by utilizing a nonlinear amplitude curve where there is a smoother transition from increasing load to constant load; e.g. an S-Curve ramp.

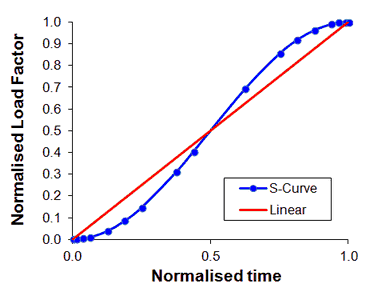
The S-Curve provides a smoother transition of the loading state at both the start and end of the load increase.

 

The equivalent ParaGeo data structure generated is Time_curve_data with the Curve_type set to 2

 

The results are visualized by plotting the high definition history data for global energy and points output in files mech_001_2d_Case1e_000.hdh and mech_001_2d_Case1e_001.hdh respectively.

 

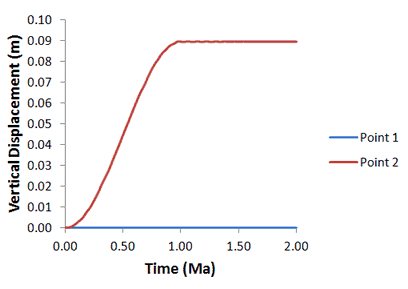
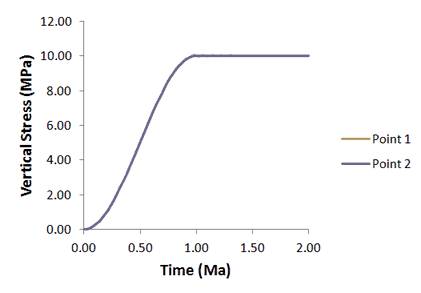
The time history of stress shows that the S-Curve ramp reduces the overshoot at time t=1.0 relative to the linear ramp case (Case 1D).

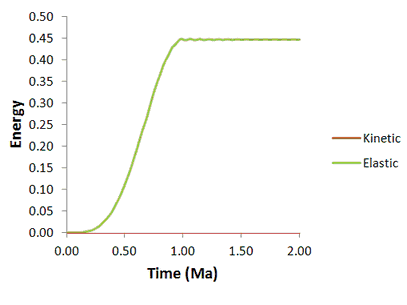
All curves exhibit only minor dynamic oscillations and the solution is close to quasi-static.   Decreasing the critical time step further would further reduce the amplitude of the oscillations at the expense of greater CPU time.