Overview of Coupling Strength

When geomechanical and flow fields are coupled they can exhibit a response ranging from relatively weakly coupled to strongly coupled depending on the properties of the sediment and the rate of loading.  The most important mechanism influencing the strength of the coupling is the rate of pore pressure generation due to volume strain.  This is influenced by several factors so that:

 

1Coupling becomes stronger as the permeability of sediment decreases; i.e. drainage time for the volume generated pore pressure change increases.

2Compressibility of the sediment increases; increasing the rate of pore pressure generation.

3The loading rate increasing; increasing the volumetric strain rate.

 

Hydrocarbon applications encompass the full range of coupling strength, for example:

 

1Wellbore stability in shales may be strongly coupled as the permeability of the shales is generally low and the rate of loading, governed by the drilling rate is high.

 

2Reservoir production simulations are often relatively weakly coupled as the permeability of the reservoir is generally quite high and often the rock experiences relatively low volume changes at low rates dictated by the production life-time and where an enhanced recovery scheme (EOR) is being used.  Local wellbore related issues during production can however still exhibit strong coupling, e.g. liquefaction of chalk due to rapid pressure changes due to shut-in events.  When the overburden shales are considered in conjunction with the reservoir their response is strongly coupled but this can generally be represented by assuming undrained conditions in reservoir-scale simulations due to the length of the drainage paths relative to the rate of loading.

 

3Geomechanical forward modelling over geological time frames often contains formations that are either weakly (sands) or strongly (shales) coupled.  The loading rate for these applications is very slow but the drainage path becomes very long with continued burial.  This disparity between permeability results in different flow regimes and flow paths in the sands and shales.  Flow through the shales, often termed primary migration, is predominantly vertical, whereas the flow through the sands, often termed flow in carriers or secondary migration, has a very high lateral component.  The rates of flow also differ greatly e.g. the flow velocity in the sands is generally > 1Km/Ma (may be much greater) whereas the flow velocity in the shale may be less than at k=10-4 mD flow may be < 20m/Ma (Hantschel and Kauerauf, 2009).  Consequently solution of the flow field in basin-modelling applications often uses a hybrid approach employing domain decomposition of the sand and shale sediment, where completely different approaches are used in each domain (Hantschel and Kauerauf, 2009).

 

 

 

Overview of Coupling Schemes

The equation system for coupled geomechanical/flow analysis can be solved using either a fully coupled approach (Lewis and Schreffler, 1998), or a sequential (staggered) solution approach (Settari and Mourits, 1998, Settari and Walters, 1999, Mainguy and Longuemare, 2002, Thomas et al., 2003, Tran et al., 2004, Dean et al., 2003, Jha and Juanes, 2007, Lewis and Sukirman, 1993). In the fully coupled method, the governing equations of flow and geomechanics are solved simultaneously at every time step. A converged solution is obtained through iteration, typically using the Newton–Raphson method (e.g. Lewis and Schreffler, 1998, Armero, 1999).

 

In the sequential approach, either the flow or mechanical problem is solved first, then the other field is solved using the intermediate solution information. An iterative process can be adopted within a sequential procedure at each time step.  This can be either a convergence based algorithm where the solution is then identical to that obtained using the fully coupled approach, or a fixed number of iterations approach with the limiting case being a staggered solution strategy with only one iteration per time step (Park, 1983, Zienkiewicz et al., 1988, Schrefler et al., 1997, Huang and Zienkiewicz, 1998).  This partitioned approach offers several advantages and is adopted in ParaGeo as it allows different solution strategies in the individual fields i.e. dynamic relaxation in the geomechanical field and implicit solution in the porous flow and thermal fields.    Two schemes are implemented for solution of coupled geomechanical/flow problems:

 

Undrained split

In the undrained split the mechanical field is generally solved using an undrained assumption to give a change in pore pressure at the intermediate stage.  The pore pressure is then computed using the volumetric strain computed in the mechanical step.  This then replaces the intermediate step pore pressure which is discarded.  The undrained assumption gives an over-estimate of the pore pressure generated in a step as some flow is expected even in low permeability formations, and consequently an under-estimate of the volume change.   This leads to a more conservative approach with greater stability than the drained split (as commented by many researchers).

 

Fixed stress split

In the fixed stress approach the volumetric loading term in the flow fluid is recast to give an additional contribution of the rock compressibility to the storativity matrix and a loading term dependent on the rate of change of total mean stress.  The seepage field is then solved first using the total mean stress rate from the previous step and then the mechanical field is solved using drained assumptions and prescribed pore pressure.  

 

Note that:

1The undrained approach is most advantageous for low permeability formations where the pressure-diffusion is relatively low.

2The fixed stress split is the most advantageous formation for higher permeability formations where the pressure-diffusion is high.

 

Coupling of the geomechanical and porous flow fields is achieved by  treating the geomechanical field as an incremental analysis with the coupling time step length corresponding to the time step of the porous flow field; i.e.

1A single porous flow step is performed in each time step for the coupled problem.  

2Multiple time steps (iterations) are performed to achieve the explicit solution (dynamic relaxation) of the geomechanical field.

This is necessary as the geomechanical and porous flow fields are "strongly coupled" due to the dependence of pore pressure on the volumetric strain rate.  

 

 

 

Undrained Split Approach

In the undrained split approach the flow field is solved first using the standard equations:

 

 

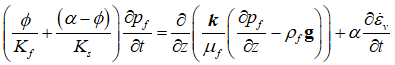
Where the volumetric strain rate is evaluated as follows:

 

 

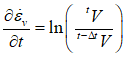
Where and are the volumes at the beginning and end of the previous coupling step respectively. Then solving the flow equation has given the change in pore pressure over the coupling time step and the pore pressure at the end of the current coupling step can be updated as:

 

 

 

Then the mechanical field is solved (several mechanical time steps for the current coupling step) with the mechanical field estimated pore pressure being updated assuming undrained conditions as:

 

 

With:

 

         ,        

 

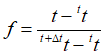
and:

          ,        

 

 

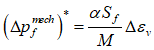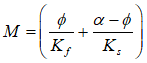
Where:

 

 

Note that factor ensures a smooth transition from the pore pressure calculated at the beginning and the end of the current coupling step. See the plot below for a schematic representation of the mechanical and porous flow field pore pressures.

 

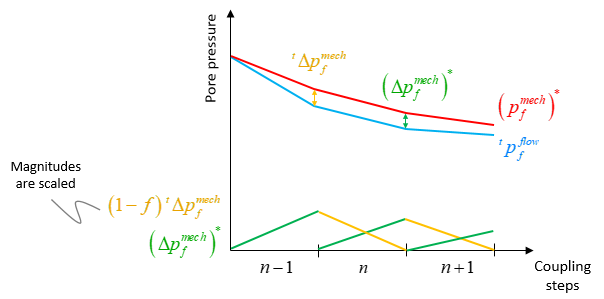
Schematic representation of the evolution of geomechanical and fluid flow pore pressures during three coupling steps. The arrows indicate the magnitudes of the indicated parameters for time step "n". The graph below show the evolution of the two parameters during the three coupling steps. Note that the magnitude has been scaled for the sake of better visualisation.

 

 

 

Fixed-Stress Approach

The governing equation for a single-phase saturated flow field in porous media can be written as:

 

 

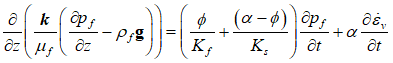
For elastic material response, the relationship between total pressure, pore pressure and strain is defined by:

 

 and hence

 

Where:

 

Note that compressive stress is negative and compressive pore pressure is positive.  Then derivation of the previous equation with time gives:

 

 

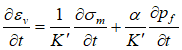
And substitution into the porous flow equation defined above gives:

 

 

 

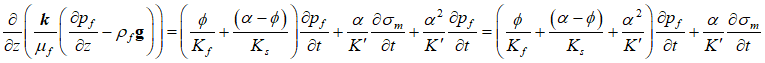
The key points of the fixed-stress approach are:

 

1.The storativity term is 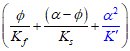 instead of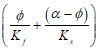

 

2.The volume strain rate term is instead of

 

3.The contribution of the volumetric strain to pore pressure generation is therefore split into two components, with one component augmenting the storativity matrix which represents the compressibility of the rock.  The magnitude of the second component is then dependent on the change in total stress.

 

4.The modification to the storativity matrix effectively accounts for the storage potential of matrix deformation leading to a more accurate prediction of the pore pressure generation.

 

5.This allows the mechanical problem being solved using the drained properties so that:

 

   where         and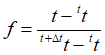    

 

6.For the fixed stress split method the pore pressure field is solved first with the rate of change of total stress taken as the average value from the previous increment i.e:

 

 

 

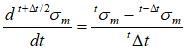
7.For coupled schemes involving explicit time stepping or dynamic relaxation the drained bulk modulus is replaced by the drained bulk modulus for the coupling step which is evaluated as:

 

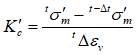    with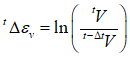    

 

 

 

Volume update model for the Undrained Split

To improve the accuracy and stability of the undrained split coupling algorithm an approximate undrained stiffness accounting for seepage in the flow field is calculated as:

 

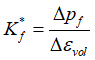
This approach is active for the undrained split with a constant undrained stiffness during the coupling step. An option to adopt a variable stiffness on a group basis calculated using the average pore pressure change in the previous coupling step (flow field change). This can be set using the Volume_update_model keyword.

 

 

•Example:

 

Lets consider that the reference fluid stiffness and the increment in volume strain in a step are:

 

  and  

 

Then the mechanical pore pressure is calculated as:

 

 

Then lets consider that the flow field pore pressure (accounting for seepage) is:

 

Then in next mechanical step the undrained stiffness is updated as:

 

 

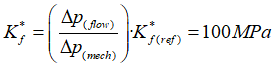
And hence the mechanical field predicted pore pressure is improved (in this example takes the same value as the flow field pore pressure) providing more stability in the algorithm: