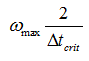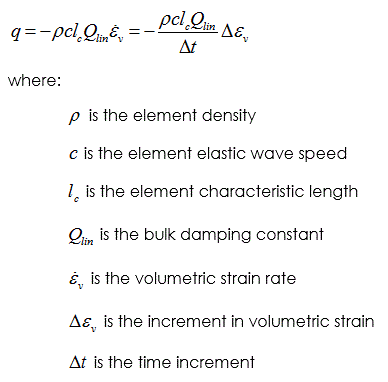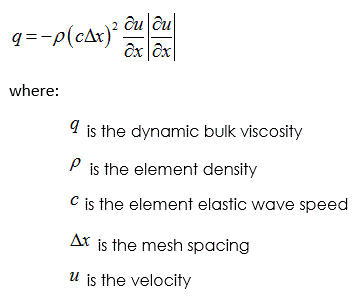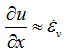Damping_global_data
Data Structure: Damping_global_data |
|
Description |
"Global Damping data" data structure for the geomechanical field |
Usage |
Damping_global_data NUM=ival where ival is the data structure number |
Description |
Overview The Damping_global_data data structure defines percentage damping that is applied to all nodes in the problem domain based on an estimated value of the lowest vibration frequency computed using the Rayleigh quotient.
Notes •Only one Damping_global_data data structures may be specified and re-specification will overwrite the existing data structure Several damping models are available:
Mass Proportional Damping It is defined via Percentage_damping and works in the same way as defined in Damping_nodal_data but applied to all the nodes in the domain. The prescribed percentage of damping is a mass proportional damping defined in the form: C =α*M Or in given the diagonal form of the mass matrix:
The lowest frequency ( Ωmin) of the current deformation mode can be estimated by the Raleigh quotient defined as:
The upper bound of the oscilation frequencies is defined by the critical time step as:
The frequency used in the evaluation of mass proportional damping is the minimum frequency evaluated by the two methods above. This constraint is applied to prevent inappropriate frequencies that may result if the approximation fort Kij is poor (e.g. due to local instabilities). The proportionality constant ( α) is evaluated every time step so that the fluctuating effective stiffness of the system is accounted for. Higher frequencies are damped more strongly than lower frequencies and so diminish first and consequently α tends to a constant value as the quasi-static solution is approached.
Notes •Only one Damping_global_data data structure may be specified and re-specification will overwrite the existing data structure •Note that Damping_global_data may be defined to specify default damping values for all the domain which may be locally overwritten by the values specified in Damping_nodal_data assigned to specific materials, groups or geometry entities. •Percentage damping is specified in the range 0 < damp < 1, where 0.1 corresponds to 10% damping of the lowest eigenvalue •Generally percentage damping is specified in the range 0.01 - 0.03. If larger values of damping are specified they can result in significant over-damping of higher modes
Bulk Viscosity Model It is defined via the keyword Bulk_damping_model. The standard dynamic bulk viscosity concept can also be used to provide volume damping in quasi-static simulations solved using an explicit solver. In this case the objective is to minimise oscillations in the effective mean stress and only the linear term of the standard bulk viscosity concept is required; i.e. the dynamic bulk viscosity ( q) for each element is defined as:
Damping is only applied in compression, so assuming elasticity, the contribution of the volumetric stress to the element internal forces is evaluated as:
This increases the resistance to deformation in compression effectively providing damping during volume decrease and no damping during volume increase. Two important properties of the algorithm are: •1) The model does not damp rigid body motion, so that the gross downward movement resulting from compaction of a column, or upward movement on a thrust, remain little affected. •2) The damping term is transitory (i.e. it is not accumulated) so if the overall deformation pattern is compressive then this mode of deformation is damped but not prevented.
Notes •Bulk viscosity damping increases the stiffness of the system and consequently reduces the critical time step necessitating more time steps •Qlin =0.5 is a suitable value for many quasi-static problems
Artificial Bulk Viscosity Model Artificial bulk viscosity (Stowe et al., 2015 for review) is a bulk (or volume) based damping designed to smooth high frequency oscillations in the dynamic simulation of shock waves. It is applied by default in all ParaGeo simulations unless Bulk_damping is defined. The formulation is based on von Neumann et al. (1950) who introduced a pressure viscosity term in their work with one dimensional shock propagation:
This dynamic bulk viscosity is positive for compressive strain rates (i.e. δu/δx<0) and negative for rarefactions. Typically, numerical implementations of such shock viscosities only activate the term for compressive strain rates. The one-dimensional viscosity of Von Neumann and Richtmyer is both effective and deceptively simple. In one dimension the strain rate across the shock, and hence velocity jump, is defined as:
In expanding this concept to two or three dimensions, the element length is replaced by the square root of the element area in two dimensions, or the cube root of the volume in three dimensions. The strain rate across the shock is approximated as the trace of the strain rate tensor:
The standard form of the shock viscosity used in many explicit codes today is a combination of the quadratic term proposed by Von Neumann and Richtmyer for strong shocks and a linear term for treating small oscillations that occur after the shock:
Notes •By default in ParaGeo the dimensionless constant are set to Qlin=1.5 and Qquad=0.06. It is not recommended to change these values.
Examples demonstrating the usage of Damping_global_data include: •damp_2d4n_001c •damp_2d4n_001e |
| Damping_models Active damping models |
Usage |
|||||||||||||||
|
|||||||||||||||
Description |
|||||||||||||||
List of active damping models. Valid models are: • "Percentage" - Percentage velocity damping • "Bulk" - Bulk damping model
Notes •Damping_models must be specified if both "Percentage" and "Bulk" models are active. •If Damping_models is not specified then Bulk damping is used in preference to Percentage_damping if both are specified.
|
|||||||||||||||
| Percentage_damping Global damping factor (0 < damp < 1) |
Usage |
||||
|
||||
Description |
||||
Global damping factor (0 < damp < 1). Generally percentage damping is specified in the range 0.01 - 0.03. If larger values of damping are specified they can result in significant over-damping of higher modes.
|
| Velocity_smoothing_damping Damping factor for velocity smoothing algorithm (0 < damp < 1) |
Usage |
||||
|
||||
Description |
||||
The damping factor for the velocity smoothing algorithm must be in the range (0 < damp < 1).
|
| Bulk_damping_type Model number for bulk damping |
Usage |
||||
|
||||
Description |
||||
The model number for bulk damping. Valid model numbers are: • 0 - No bulk damping (default) • 1 - Linear bulk viscosity model • 2 - Viscous damping based on the bulk stiffness
|
| Bulk_damping_model Model name for bulk damping |
Usage |
||||
|
||||
Description |
||||
The model name for bulk damping. Valid model names are: • "None" - No bulk damping (default) • "BulkViscosity" - Linear bulk viscosity model • "BulkStiffness" - Viscous damping based on the bulk stiffness
|
| Bulk_damping_properties Bulk damping properties |
Usage |
|||||||||||||||
|
|||||||||||||||
Description |
|||||||||||||||
The bulk damping properties are model dependent.
Model 1 - Bulk viscosity model The poroelastic parameters are: • Location 1 - Bulk viscosity constant ( Qlin) (Default 0.5)
Model 2 - Viscous damping based on the bulk stiffness The poroelastic parameters are: • Location 1 - Bulk stiffness factor ( Fbulk)
|
|||||||||||||||