Ex_006 Eulerian boundaries
This example demonstrates how to use eulerian boundaries to add or remove sediment volume from the system. The eulerian algorithm works as follows:
1.An inflow/outflow sediment velocity is prescribed for the eulerian boundary.
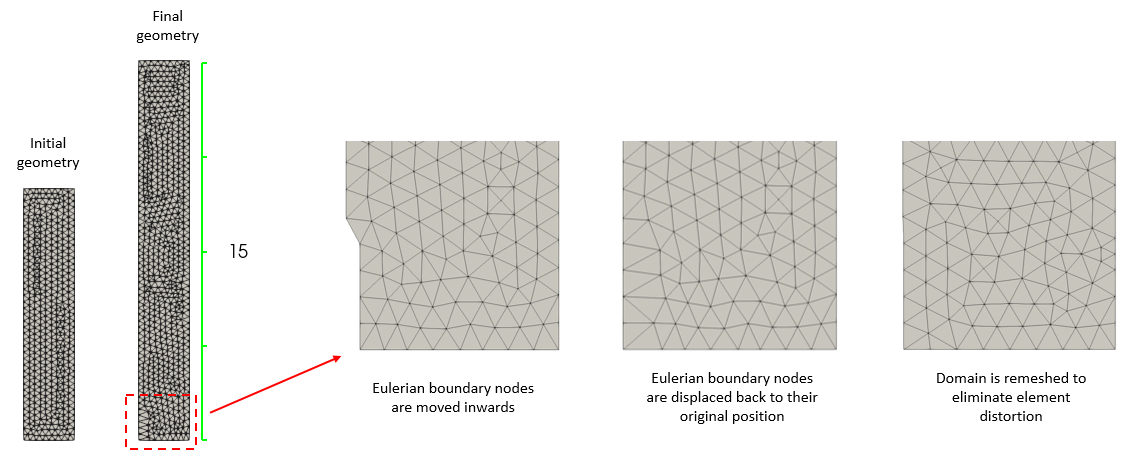
2.The eulerian boundary nodes are moved in / out of the domain according to the prescribed velocity.
3.Then the nodes are pulled back to their original position and the domain is remeshed. This occurs every n time steps as defined by the user.
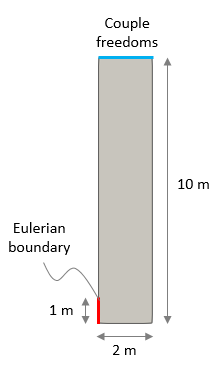
For demonstration of usage of eulerian boundaries a simple column geometry will be used. The column is initially 10 m high and 2 m wide. A 1 m eulerian boundary is defined in the bottom part of the column's western boundary. The material is modelled using a viscoplastic rheology. Gravity is applied during the first stage of 1 Ma. Then a second stage considering inflow/outflow of sediment during 10 Ma at a specified velocity is performed. Note that quite frequent adaptivity checks are required for eulerian boundaries. Note also that the top surface is constrained with Couple_freedoms to ensure that the vertical displacement is homogeneous as the sediment is added / removed from the domain. Because of the simple geometry and conditions it is straightforward to calculate the expected final column height at the end of the simulation.
Initial geometry
The data files for the examples are found in: ParaGeo Examples\General Examples\Ex_006\Data
Case1: Inflow of salt
Case2: Outflow of salt
Case3: Free eulerian boundaries
|
| Results |
The result files for the project are in directory: ParaGeo Examples\General Examples\Ex_006\Results.
For the present example it is straightforward to calculate the expected final column height. In case 1 the injection velocity was prescribed to 1 m/Ma and inflow occurred during 10 Ma. The eulerian boundary is 1 m high and the column width is 2 m. Hence the expected increase in height can be calculated as Δh = 1 m/Ma · 10 Ma · 1 m / 2 m = 5 m. In the figure below it can be seen that the final column height is approximately 15 m so it has increased 5 m as expected.
In the figure it is also shown the sequence combining the eulerian boundary algorithm with remesh used to simulate salt injection. It should be noted that the additional volume is introduced in the system when the nodes are pulled back to their original position.
Results for Case 1 (prescribed salt inflow) with detailed sequence of eulerian boundary and remesh update
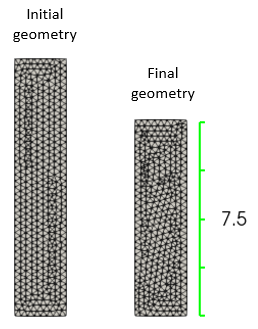
In case 2 the injection velocity was set to -0.5 m/Ma in order to simulate salt outflow from the domain. A decrease of 2.5 m in column height is expected and as can be seen in the figure below the results match that height increment.
Results for case 2 (prescribed salt outflow)
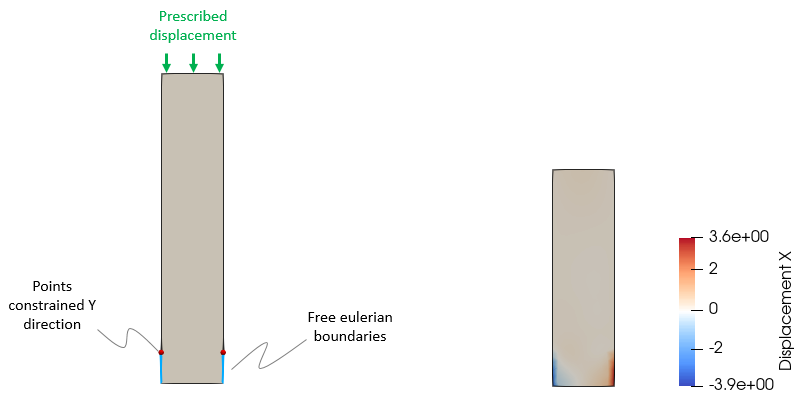
In case 3 two free eulerian boundaries at the bottom of both sides of the column are considered. A prescribed downward displacement of 3 m is applied to the top surface. The upper points of the eulerian boundaries are constrained in the Y direction in order to avoid closure of the eulerian boundary as salt is evacuated and the downward displacement progresses. In the horizontal displacement results it can be seen that the free eulerian boundaries allowed for salt evacuation as the salt was subjected to vertical compression.
Schematic of boundary conditions (left) and horizontal displacement results (right)
Note that volume inflow/outflow from the domain is monitored in the .res file. For case 3 for example it can be seen that from an initial volume of 20 m3 due to a vertical downward displacement of 3 m the column has lost 6 m3 and is 14 m3 at the end. It can be seen that every eulerian boundary has evacuated almost 3 m3 of salt.
.res file
|
||||