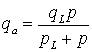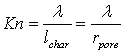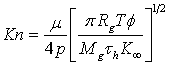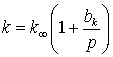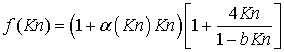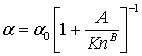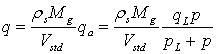Gas flow

Single-phase compressible gas flow through porous media is represented by augmenting the standard porous flow equations so that several additional mechanisms are represented.  These include:

1        Fully compressible treatment of gas phase via a gas equation of state.

2        A flow model that accommodates a wide range of fundamental flow mechanisms; i.e. continuum, slip, transition, and free molecular flow, depending on the Knudsen number.

3        Adsorption/desorption model for transfer of gas between the shale and gas phases.

 

 Click to expand/collapseGas Equation of State

The real-gas equation of state is defined as:

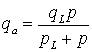
gas_flow_adsorpt_001

where

Z

 

is the real gas deviation factor (dimensionless) which may be dependent on pressure Z ≤ 1.0

 

T

(K)

is the temperature,

 

Mg

(kg/kmol)

is the molecular mass of the gas

 

Rg

(J/mol/K)

is the universal gas constant.

Representation of isothermal gas adsorption/desorption using the Langmuir isotherm requires specification of the following parameters in the Fluid_properties data structure:

 

  Equation_state_type                  Integer_value   ! Type 1 - Real Gas equation of state

  Equation_state_properties IDM=2

      /Gas deviation factor/              Real_value   ! Z <=  1.0

      /Minimum allowable pressure/        Real_value   ! A low non-zero pressure e.g. 1 Pa

  Gas_universal_constant                  Real_value   ! Gas Constant (J/Kmol/K)

  Molecular_weight                        Real_value   ! Molecular Weight (Kg/Kmol)

 

 

 Click to expand/collapseGas Flow Mechanisms

Flow mechanisms vary according to Knudsen number (Kn), which is a measure of the degree of rarefaction of gas flow through small pores, and is defined as:

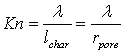
gas_flow_knudsen_001

where

λ

is the mean free path of molecules

 

lchar

is the representative path; e.g. the mean hydraulic radius rpore.

Kinetic theory for a perfect gas may be used to derived expressions for λ. For example the expression adopted by Civen et al. (2011) leads to

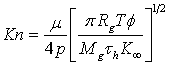
gas_flow_knudsen_002

where

μ

Pa s

is the viscosity of gas

 

p

Pa

is the absolute gas pressure

 

Rg

J/kmol/K

is the universal gas constant

 

T

K

is the absolute temperature

 

Mg

kg/kmol

is the molecular mass of gas

 

τh

 

is the tortuosity

The Knudsen number relates pore structure to flow regime, which can be visualized for a shale-gas formation in the figure below.  This shows that Darcy flow is usually dominant in the high-permeability fractured zone adjacent to the wellbore, whereas free molecular or transition flow may be dominant provided the porosity of the shale is sufficiently low.

Gas-Shale Stoage and Flow Capacity Diagram (Sondergeld et al., 2010)

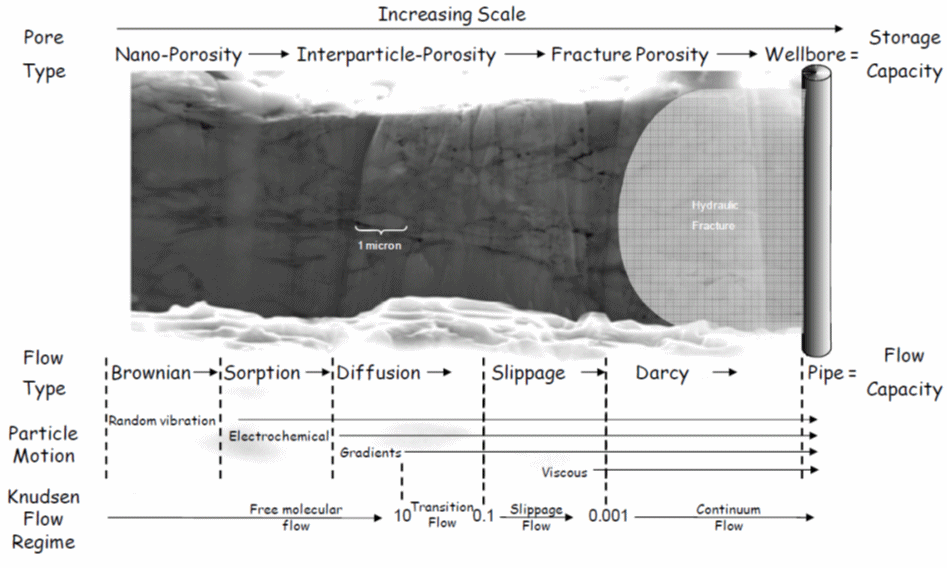Gas-Shale Stoage and Flow Capacity Diagram (Sondergeld et al., 2010)

The flow regimes is also dependent on gas pressure, as the Knudsen number is inversely proportional to gas pressure.  This is evident from the plot of Knudsen number vs. gas pressure below, where the typical conditions found in conventional, tight-gas and shale-gas reservoirs are also shown (Freeman et al., 2011)

Flow Regimes in Tight-Gas and Shale-Gas Reservoirs (Freeman et al., 2011)

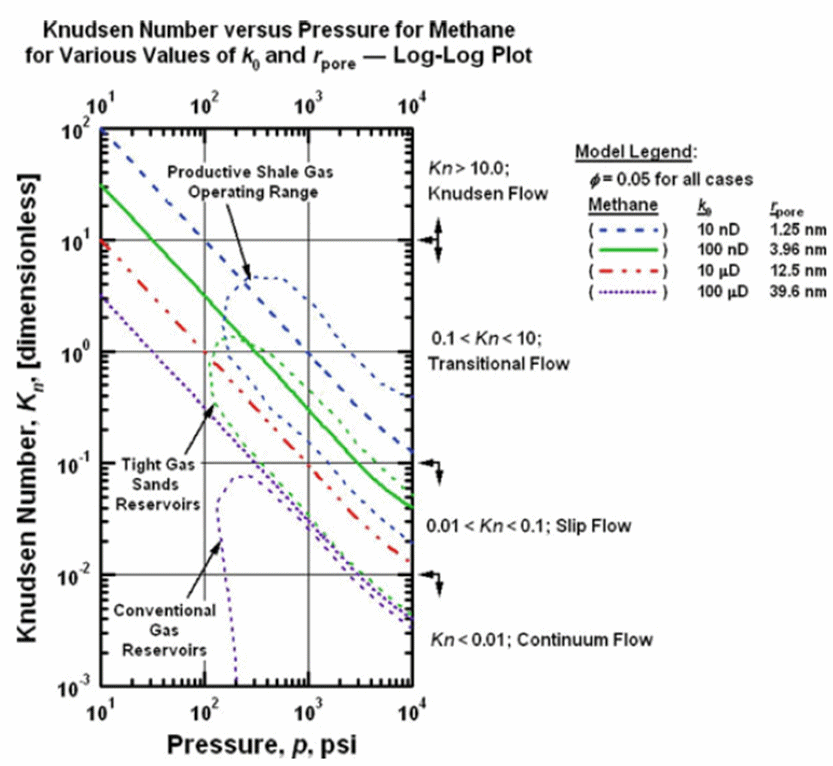Flow Regimes in Tight-Gas and Shale-Gas Reservoirs (Freeman et al., 2011)

Four types of flow regimes are generally identified for different Knudsen number ranges:

Flow Regime

Knudsen Range

Description

Continuum

(Kn < 0.01)

The mean free path of the gas molecules is negligible compared to the characteristic dimension of the flow geometry

Slippage Flow

(0.01 < Kn < 0.1)

The slippage phenomenon occurs in the layer of molecules immediately adjacent to the boundary walls

Transition Regime

(0.1 < Kn < 10)

 

Molecular Flow Regime

(Kn > 10)

The flow is dominated by diffusive effects

 

 

 Click to expand/collapseKnudsen Diffusion Models

Gas slippage is generally represented by an effective permeability law which may be written in the form:

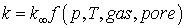
gas_flow_knudsen_003

where k∞  is the absolute permeability of the sample.  Several different forms of this model are implemented including:

•The Klinkenberg Model (Klinkenberg, 1941)

•The Beskok and Karniadakis Model ( Beskok and Karniadakis, 1999)

 

The Klinkenberg model Klinkenberg (1941) provides  a first order correction for gas slippage the equivalent permeability (k) is defined as:

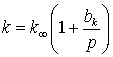
gas_flow_knudsen_004

where

k∞

is the absolute permeability

 

bk

is the gas slippage factor which is a function of the mean free path (λ) of the molecules at the mean pressure (p) and effective pore radius (r)

The data input required for the Klinkenberg model is

  Knudsen_diffusion_type                 1    ! (1-Klinkenberg)

  Knudsen_diffusion_data IDM=1

      /Slippage factor b/            Real_value

 

 

Beskok and Karniadakis (1999) derived a second order accurate expression for permeability by studying rarefied gas flows in channels, pipes, and ducts with smooth surfaces in a wide range of Knudsen number (Kn) at low Mach number (M).  They propose an expression of the form

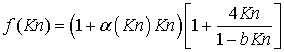
gas_flow_knudsen_005

where

b

is the slippage coefficient (Civan et al., 2011), which is different from bk in the Klinkenberg model, and generally assumed to have a value of -1

 

α

is the rarefaction coefficient

The rarefaction coefficient (α) varies in the range 0 < α < α0 for 0 < Kn < ∞ (Beskok and Kaniadiakis, 1999) and Civan et al. (2011) suggests a relationship of the form

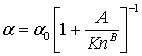
gas_flow_knudsen_006

where A and B are empirical constants.  These constants must be determined either numerically or experimentally by regression analysis of flow at different Knudsen number for each given class of channel geometry, as A and B depend on the flow channel shape.  An extensive discussion on the determination of α is presented by Beskok and Kaniadiakis (1999).

The data input required for the Beskok and Karniadakis model is:

  Knudsen_diffusion_type                 2    ! (2-Beskok Model)

  Knudsen_diffusion_data IDM=4

      /Rarefaction Coeff. Alpha0/    Real_value

      /Constant A/                   Real_value

      /Constant B/                   Real_value

      /Slippage factor b/            Real_value

Additionally the following must be defined to enable evaluation of the Knudsen Diffusion coefficient

  Totuosity                               Real_value   ! Type 1 - Real Gas equation of state

  Gas_universal_constant                  Real_value   ! Gas Constant (J/Kmol/K)

  Molecular_weight                        Real_value   ! Molecular Weight (Kg/Kmol)

 

 

 

 Click to expand/collapseGas Adsorption/Desorption - Langmuir Isotherm

The Langmuir isotherm (e.g. Civan et al., 2011; Qu et al., 2012) relates the coverage or adsorption of molecules on a solid surface to gas pressure or concentration of a medium above the solid surface at a fixed temperature. The Langmuir isotherm is defined as:

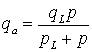
gas_flow_adsorpt_001

which can be expressed as

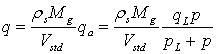
gas_flow_adsorpt_002

where

ρs

(kg/m3)

is the grain density

 

q

(kg/m3)

is the mass of gas adsorbed per solid volume

 

qa

(std m3/kg)

is the standard volume of gas adsorbed per solid mass

 

qL

(std m3/kg)

is the Langmuir gas volume

 

Vstd

(std m3/kmol)

is the molar volume of gas at standard temperature (273.15K) and pressure (101.325Pa)

 

p

(Pa)

is the gas pressure

 

pL

(Pa)

is the Langmuir gas pressure

 

Mg

(kg/kmol)

is the molecular weight of gas

Representation of isothermal gas adsorption/desorption using the Langmuir isotherm requires specification of the following parameters in the Fluid_properties data structure:

 

  Adsorption_type                        1    ! Langmuir Isotherm

  Langmuir_volume               real_value    ! (q(L)) (m3/kg)

  Langmuir_pressure             real_value    ! (p(L)) (Pa)

  Std_molar_volume              real_value    ! Standard molar volume (V(std)) (m3/kmol)

  Molecular_weight              real_value    ! Molecular Weight (Kg/Kmol)