Algorithm Concept

The Nearest Neighbour algorithm (Sambridge (1999a, b)) is used to solve nonlinear inverse problems. This optimisation algorithm is a direct search (derivative-free) method in the same class of inversion techniques such as Simulated Annealing and Genetic Algorithms. These methods are similar in that they use randomized decisions in exploring the multidimensional parameter space. The complexity of the cost or objective function is the limiting factor since its derivatives are not required to guide the search.

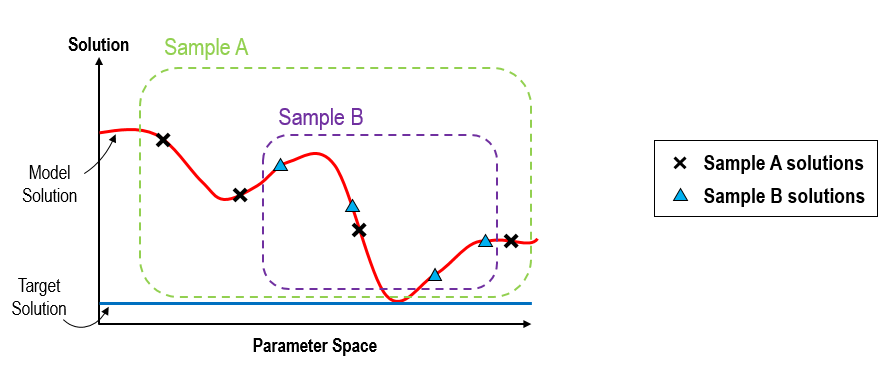
During the search process, the Nearest Neighbour algorithm identifies the models with best solutions (lower misfit value) from the current sample of models in order to perform a resample (generation of a new sample of models). For example, in figure shown below, "Sample B" is contained within "Sample A" because previously solutions for models in "Sample A" were ranked and the best 3 were chosen to generate "Sample B"  what has allowed to get closer to the target solution.

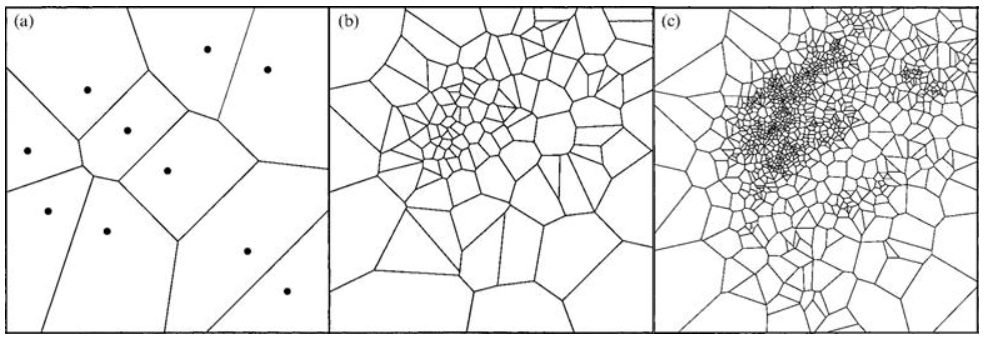
There are two major stages, i.e. search and appraisal stage. In search stage, Voronoi cells are used to partition the parameter space. A model inside each cell is generated and solved. Then solutions are appraised and ranked based on the misfit value relative to a target solution. Then a subset consisting on the best models (the ones with lower misfit value) are used to perform a resample. With each resample, the new generated models concentrate on the cells with relatively lower misfit relative to the rest of the cells, as illustrated below. Starting from 10 quasi-random points and the associated Voronoi cells, the first 100 samples are generated using the neighbourhood approximation, followed by 1000 samples.

Unlike other optimisation algorithms like the Simulated Annealing method which requires a number of tuning parameters, the Nearest Neighbour algorithm only requires two parameters, which are

•Number of Voronoi cells to resample

•Number of new samples to generate in each resampled cell

The outcome of search stage is the generation of a number of ensembles. Appraisal stage is where the error analysis of ensembles of model is performed. The salient feature of the Nearest Neighbour algorithm is that inference about the system is made by using the suite of all generated models, rather than a single, lowest-misfit model. The argument is that even poor-fitting models contain information about the system.

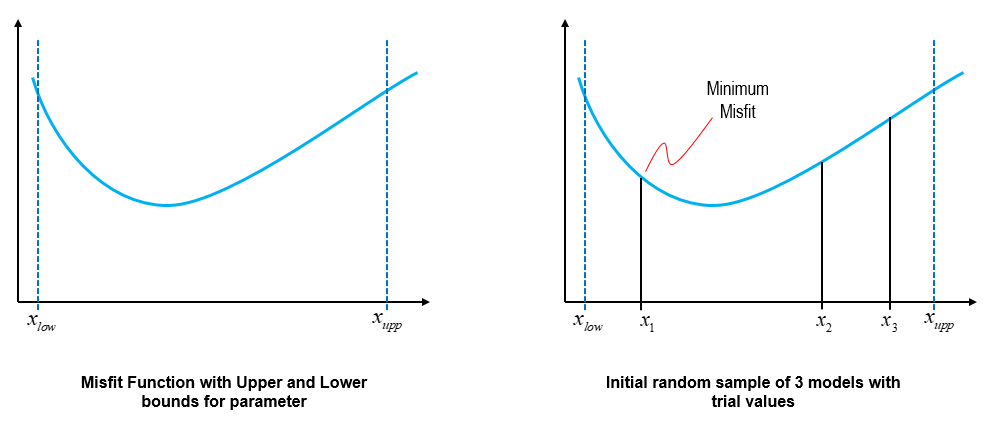
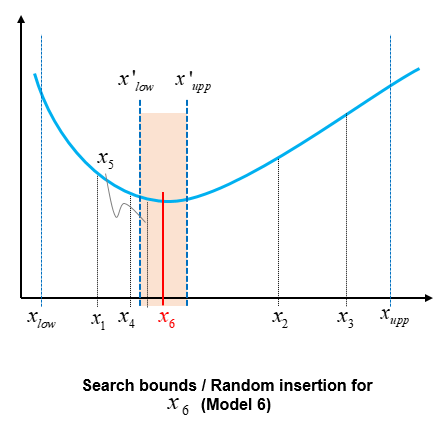
The basic concept of the Nearest Neighbour algorithm is illustrated below. Firstly, we assume the parameter space is represented by a single cell, ranging from xlow to xupp. Then, a prescribed number of points (3 in this case) is randomly placed within the cell.

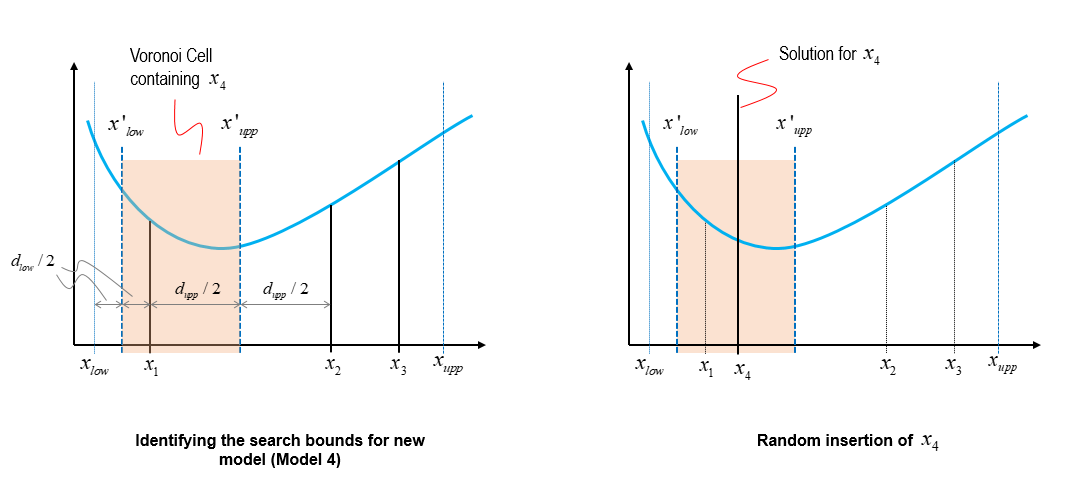
Because x1 is the minimum misfit solution in the previous cell, a new cell is constructed by defining the updated bounds x'low and x'upp based on x1 as shown below. The process is repeated by randomly placing new points in the parameter space. In this case, x4 emerges as the new solution.

The process is repeated until meeting the convergence tolerance, that is the misfit value falls below a prescribed value.