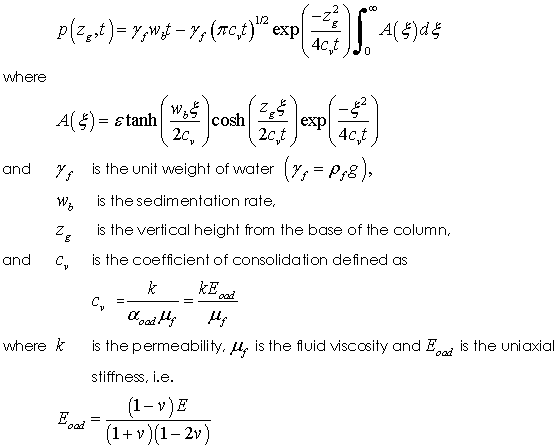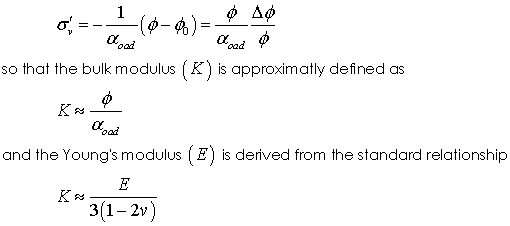HM_002 Uniaxial Sedimentation using Pre-Existing Sediment
This example extends the uniaxial consolidation example HM_001 by considering overpressure build up and dissipation during the sedimentation of a 1000m column. The 1000m column is represented as pre-existing material and gravity is ramped up slowly over the equivalent deposition time. This is used to provide a base case solution and to introduce the modelling issues. The pre-existing sediment assumptions is not valid, however, as in reality the drainage path from the base of the model to the free surface gradually increases from zero to 1000m over the deposition time. In contrast, with the pre-existing sediment the drainage path is always ca. 1000m.
This example focuses on model set up and simulation of large-scale coupled problems.
The example documentation assumes that the user is familiar with mesh generation and single field geomechanical modelling functionality and the following examples should be undertaken beforehand:
1Mech_001 Mechanical Analysis Introduction
2HM_001 Introduction to Hydro-Mechanical Analysis - Uniaxial Consolidation
Analytical Solution
Analytical equations for the development of overpressure in a basin at constant sedimentation rate were developed by Gibson (1958) and further discussed in Gibson (1967) and Wangen (2010) amongst others. The solution assumes a shallow basin where the porosity reduction is negligible; i.e. the geometrical impact of compaction may be neglected. The key assumption of the model is that porosity (φ) is a linear function of the vertical effective stress (σ'v); i.e.
Substitution in the mass conservation equation and solution for the special case of constant sedimentation rate and zero surface pore pressure then gives
Note that rearrangement of the expression for porosity gives
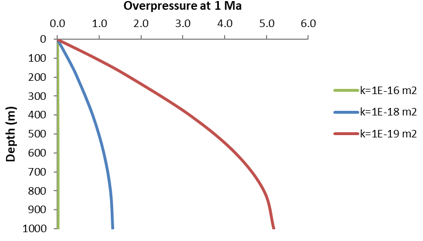
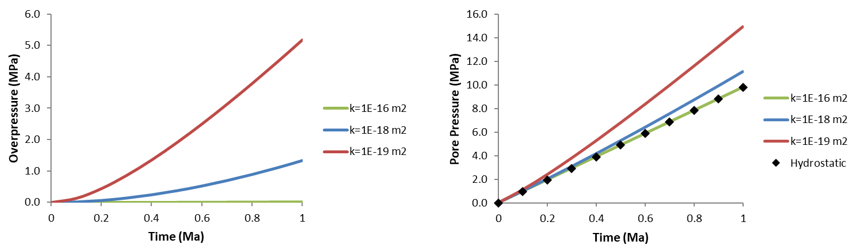
Wangen (2010, p.403) provides overpressure predictions for a particular set of material parameters comprising;
A solution, obtained by very approximate integration using a multi-point trapezoidal rule, is provided in the Excel worksheet HM_002\00_hm_002.xlsx "Analytical" worksheet.
Overpressure at 1 Ma for Three Different Permeability Values
Overpressure and Pore Pressure at the Base of the Column vs. Time for Three Different Permeability Values (Analytical)
References Gibson, R. E. 1958. The progress of consolidation in a clay layer increasing in thickness with time. Géotechnique, 8, 171–182. Gibson, R. E., England, G. L. & Hussey, M. J. L. 1967. The theory of one-dimensional consolidation of saturated clays. Géotechnique, 17, 261-273. Wangen, M. 2010. Physical Principles of Sedimentary Basin Analysis, Cambridge University Press.
|
Simulation Cases
Base Case 1 Permeability = 1E-18m2