This tutorial example aims to demonstrate the mechanical compaction models available which automatically, and internally, generate the appropriate "user-defined" hardening data for Athy-type normal compaction curves. Those mechanical compaction models greatly simplify the required user-input data to obtain a target normal compaction trend which is expected to be straightforward for those users familiar with the Athy compaction model widely used in basin modelling.

 

Currently, two mechanical compaction models are available:

 

▪Athy depth-based model model (Model 2)

 

▪Schneider model (Model 1), which is a variation of the Athy model that allows more flexibility in defining different shapes of compaction curves at the expense of requiring additional parameters

 

 

The function that defines the Athy compaction trends is written as:

 

 

Where ø is the porosity, ømin  is the residual (minimum) porosity, ød is the depositional porosity, k is the compressibility and ze is the depth.

 

The function that defines the Schneider compaction trends is written as:

 

     with    

 

Where ø is the porosity, ømin  is the residual (minimum) porosity, ød is the depositional porosity, øa is the first fraction of the depositional porosity, øb is the second fraction of the depositional porosity, ka is the compressibility associated with the øa fraction of the depositional porosity, kb is the compressibility associated with the øb fraction of the depositional porosity and ze is the depth.

 

It is noted that the Athy and Schneider models provide identical curves when ød = øa + øb and k = ka = kb. This is shown in the following figure where the curves use ød = 0.6, øa = øb = 0.3 and k = ka = kb= 0.75 1/Km :

 

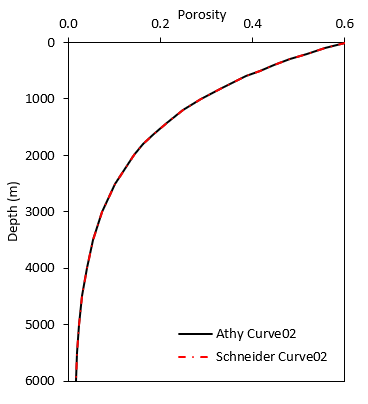
Comparison of equivalent compaction curves

 

 

As mentioned above the Schneider model adds flexibility in defining compaction curves which assume rapid compaction at shallow depths and then decreasing the amount of compaction with depth. The figures below show different Athy compaction curves which assume the same depositional porosity but  consider different compressibilities. The parameters used to generate those curves are provided in the table:

 

 

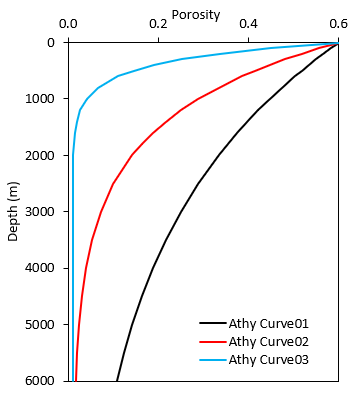
Comparison of different Athy curves for different compressibilities

 

As can be seen as the compressibility increases, for a given depth the sediment achieve lower porosity values and the minimum porosity is achieved at shallower depth. With the Schneider model, in addition to being able to replicate the same compaction trends as previously shown, there is the possibility to consider more compressibility at shallow depths but retain larger porosities at deeper depths. This is shown in the following figure where the Schneider Curve02 is equivalent to the Athy curve02 in the previous figure. Note that again all the curves consider the same depositional porosity.

 

 

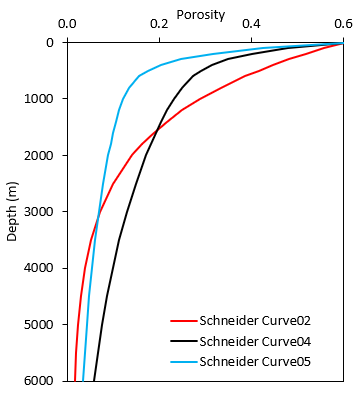
Comparison of different Schneider curves

 

 

As can be seen Curve05 considers more compaction at shallower depths relative to Curve04 as in the former, a larger portion of the total depositional porosity is affected by the large compressibility value ka . It is also noted that due to the low compressibility value set to kb , both curves retain more porosity than curve02 at 6000 m depth. The spreadsheet Mat_001d/Additional/00_Mat_001d_Intro.xlsx used to generate the previous curves is provided so that the user can experiment with the input values.