The present tutorial example aims to demonstrate the set up for using the Super Element (SE) workflow in ParaGeo. The super element is an approach that may be used to save computational time when the performance of numerous simulation variations of the same model are required (e.g. to run a sensitivity analysis, to simulate the response of the model under different conditions or when running the numerous simulations involved in an inverse analysis).

 

The super element approach is based on the reduction of degrees of freedom by substitution of part of the model domain mesh by a super element with equivalent behaviour. Basically the model can be divided into two sets of components:

 

1.Non-retained components that will be replaced by a super element

2.Retained components that will be preserved in the model

 

Then after substitution of the non-retained components by a super element the solution for the retained components must be identical to that of the original model. In other words, the super element properties are defined so that the response in the boundary or boundaries connected with the retained components is identical. This is achieved by a mathematical procedure known as "static condensation" which involves the calculation of a reduced stiffness matrix that includes the contribution of all the non-retained components.

 

Generally the non-retained components are the regions in which we are not particularly interested to solve. It should be noted that a limitation of the approach is that the non-retained components that will be substituted by a super element must behave in a linear manner (i.e. Elastically).

 

The first step of the workflow consist in the creation of the super element. To do that a partial solve is performed from which the response of the non-retained components that will become a super element is analysed. From this, the super element model matrix is determined and output in a file than can later be imported for usage in subsequent simulations.

 

In ParaGeo there is also the capability to reflate the results in the super element (i.e. to use the results obtained from the model using the super element to calculate the solution in the original mesh).

 

To demonstrate the super element workflow the present tutorial example considers a 3D model consisting of an elasto-plastic metal billet which is pushed by an elastic platten. The platten is stacked above the billet and both are initially cubic with a side size of 100 mm. The initial mesh discretisation considers 20 hexahedral elements per side (which gives a total of 16000 elements and 18081 nodes). A 10 mm downward (compressional) displacement is applied to the top surface. Normal displacements are constrained for the base, south, north and west boundaries (roller boundary condition) whereas the eastern boundary is unconstrained. The constitutive behaviour of the platten is modelled elastically whereas the metal billet is modelled via elasticity and Von Mises plasticity with hardening, both groups characterised with arbitrary properties summarised in a table below. A reference solution in which the super element approach is not used is also provided for comparison. Simulations will be performed using the implicit solver (see Imp_001 tutorial example for description of the implicit set up).

 

 

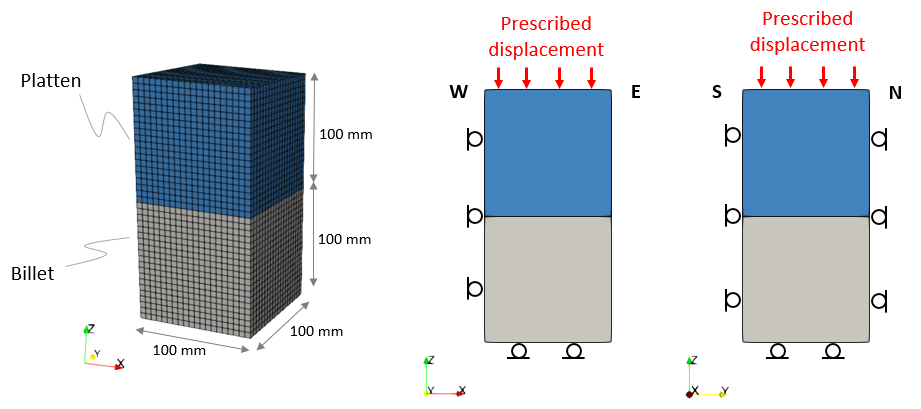
Original model mesh and boundary conditions

 

 

 

 

Table summarising material properties