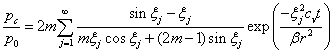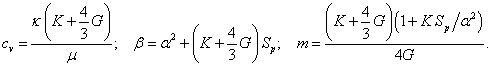Val_002b Spherical Soil Sample

Contents

Problem Description

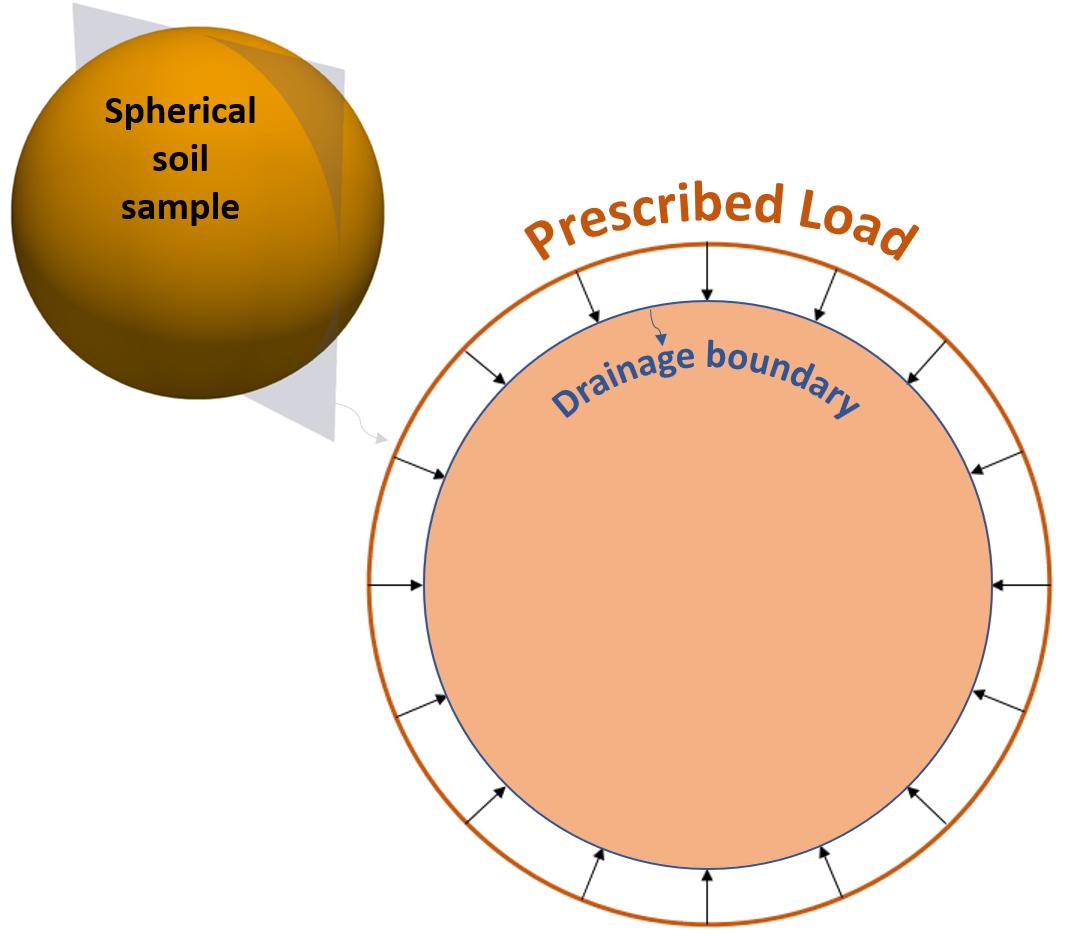
Mandel-Cryer effect is a phenomenon observed in a sample of saturated soil, which is characterised by the increase of pore pressure followed by reduction towards zero value under external load. This load is prescribed instantaneously on the sample and kept constant while drainage takes place. Such behaviour is a manifestation of overpressure generation due to impact load because the interstitial fluid cannot escape in time due to permeability and distance to the drainage boundary, and so the momentary undrained condition will resist deformation. This phenomenon has been verified experimentally by (Gibson, Knight, & Taylor, 1963) and (Verruijt, Discussion on consolidation of a massive sphere, 1965). Using the Biot’s theory of consolidation, the analytical solution of relevant problems have been derived (Mandel, 1953), (Cryer, 1963) and (Leeuw, 1965). In this section, we consider Cryer’s model, in which a spherical saturated soil sample is loaded instantaneously while the evolution of inner soil pore pressure is monitored. The only difference with the Cryer’s model is that we consider variable Biot’s coefficient (α), while the original version uses α = 1.0.

Val_02b_01

Val_02b_02

Illustration of Cryer model. External load is prescribed instantaneously and held constant. Meanwhile, the fluid within the saturated soil sample flows out of the boundary.

Mandel-Cryer effect. Momentary increase of pore pressure beyond the initial level before decreasing towards zero value. The plot shows the analytical solution predicting the evolution of pore pressure at the center of soil sample.

The analytical solution which admits variable Biot's coefficient has been derived by (Verruijt, 2008):

Val_002b_eqn1 ,

where pc is the pore pressure at the core, p0 is the initial pore pressure, t is time, r is the sphere radius, and the coefficient ξj are the positive roots of the equation

The parameters cv, m, and β are defined by

Val_002b_eqn3

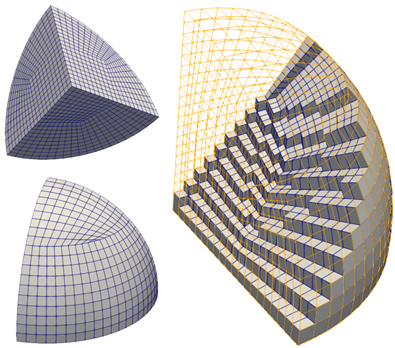
In the current simulation model, only a quarter of the spherical soil sample is modelled due to symmetry. The domain is discretised into 4000 hexahedral elements (with Bbar formulation), which consists of 4641 nodes. The instantaneous load is 1 MPa, which is kept constant throughout the simulation time.

Val_02b_03

Discretised model of Cryer's model using hexahedral elemtns with Bbar formulation.

The material properties and geometry information are listed as follows.

Property	Value
Grain stiffness (MPa)	38000
Grain density (kg/m3)	2650
Porosity	0.2
Young's modulus (MPa)	10
Poisson's ratio	0.33
Hydraulic permeability (m2)	4.95(10-9)
Biot coefficient	1.0
Fluid stiffness (MPa)	2000
Fluid viscosity (MPa.s)	10-5
Fluid density (kg/m3)	1000
Radius (m)	1.0

The data file for the model is found in: ParaGeo Examples\Validation\Val_002\Data\Val_002b.dat.

Data File

* Geometry_data NUM=1

! -----------------------------

File_name Mandel.geo

File_format hdf

* Geometry_set NUM=1

! ------------------------------

Name "load_surf"

Set_type "Abaqus NSET"

Surfaces IDM=1

* Geometry_set NUM=2

! ------------------------------

Name "base"

Set_type "Abaqus NSET"

Surfaces IDM=1

* Geometry_set NUM=3

! ------------------------------

Name "side_x"

Set_type "Abaqus NSET"

Surfaces IDM=1

* Geometry_set NUM=4

! ------------------------------

Name "side_y"

Set_type "Abaqus NSET"

Surfaces IDM=1

* Geometry_set NUM=5

! ------------------------------

Name "Mandel"

Set_type "Group"

Volumes IDM=1

! ---------------------------------

! Group data

! ---------------------------------

* Group_control_data

! ---------------------------------

Group_numbers IDM=1

Active_geomechanical_groups IDM=1

Active_porous_flow_groups IDM=1

* Group_data NUM=1

! --------------------------------------

Group_name "Mandel"

Element_type "HEX8"

Material_name "Poroelastic"

Volumes IDM=1

Porous_flow_type 4

!----------------------------------

! Material Data

!----------------------------------

* Material_data NUM=1

! ---------------------------------

Name "Poroelastic"

Units IDM=4

MPa

Celsius

Grain_stiffness 38000.0

Grain_density 2650.0

Porosity_model_type 1

Porosity 0.2

Elastic_model_type 1

Isotropic_elastic_properties IDM=2

/"Young's Modulus (E)"/ 10.0

/"Poisson's Ratio (v)"/ 0.33

Singlephase_fluid_name "Water"

Permeability_type 1

Permeability 4.95E-09

Biot_type 1

Biot_properties IDM=1

1.0

* Fluid_properties NUM=1

! ---------------------------------

Name "Water"

Fluid_type "Water"

Equation_state_type 0

Stiffness 2000.0

Density 1000.0

Viscosity_type 1

Viscosity 1.00E-5

!----------------------------------

! Boundary conditions

!----------------------------------

* Support_data

! ---------------------------------

Displacement_codes IDM=3 JDM=4

/Set 1/ 1 0 0

/Set 2/ 0 1 0

/Set 3/ 1 1 0

/Set 4/ 1 1 1

Displacement_code_geom_set IDM=1

'Mandel'

Displacement_code_geom_ass IDM=1

Pore_pressure_codes IDM=1 JDM=2

1 ! Prescribed

0 ! Free

Pore_pressure_code_geom_set IDM=1

'Mandel'

Pore_pressure_code_geom_ass IDM=1

* Time_curve_data NUM=1

! ---------------------------------

Time_factor IDM=2

0.0 1.0

Time_curve IDM=2

0.0 0.01

* Global_loads NUM=1

! ---------------------------------

Prescribed_pore_pressure IDM=1 JDM=1

/Set 1/ 0.001

Pres_pore_pressure_geom_set IDM=1

'Mandel'

Pres_pore_pressure_geom_ass IDM=1

* Load_case_control_data

! ---------------------------------

Loadcases IDM=1

Active_load_flags IDM=1

! --------------------------------------

! Damping data

! --------------------------------------

* Damping_global_data

! --------------------------------------

Percentage_damping 0.02000

Bulk_damping_model "BulkViscosity"

Bulk_damping_properties IDM=1

0.500000

! --------------------------------------

! Coupling control data

! --------------------------------------

* Couple_control_data

! --------------------------------------

Solution_algorithm "Incremental"

Volume_strain_coupling "Fixed_stress"

Volume_update_model "Variable_group"

Field_names IDM=2

"Geomechanical"

"Porous_flow"

! ======================================

! Stage 1: Initialisation

! ======================================

* Time_scaling_factors

! --------------------------------------

Optimal_time_step 1E-3

* Control_data

! --------------------------------------

! General setup

Control_title "Initialisation"

Solution_algorithm 7

! Coupled incremental data (Flow step)

Maximum_number_time_steps 1E8

Duration 0.1

Initial_time_increment 5E-3

! Geomechanical iteration data

Maximum_number_iterations 5000

Factor_critical_time_step 0.9

! Tolerance

Displacement_norm_tolerance 0.01

! Output Data

Screen_message_frequency 100

Output_frequency_plotfile -1

! ======================================

! Stage 2: Loading

! ======================================

! --------------------------------------

! Boundary conditions

! --------------------------------------

* Support_data

! ---------------------------------

Displacement_codes IDM=3 JDM=4

/Set 1/ 1 0 0

/Set 2/ 0 1 0

/Set 3/ 0 0 1

/Set 4/ 0 0 0

Displacement_code_geom_set IDM=3

base

side_x

side_y

Displacement_code_geom_ass IDM=3

Pore_pressure_codes IDM=1 JDM=2

1 ! Prescribed

0 ! Free

Pore_pressure_code_geom_set IDM=1

'load_surf'

Pore_pressure_code_geom_ass IDM=1

* Time_curve_data NUM=1

! ---------------------------------

Time_factor IDM=2

1.0 1.0

Time_curve IDM=2

0.01 500000.0

* Global_loads NUM=1

! ---------------------------------

Prescribed_pore_pressure IDM=1 JDM=1

/Set 1/ 0.0 ! MPa

Pres_pore_pressure_geom_set IDM=1

'load_surf'

Pres_pore_pressure_geom_ass IDM=1

* Time_curve_data NUM=2

! ---------------------------------

Time_factor IDM=2

1.0 1.0

Time_curve IDM=2

0.01 500000.0

* Global_loads NUM=2

! ---------------------------------

Surface_load IDM=3 JDM=1

/Set 1/ 1.0 0.0 0.0

Surface_load_geom_set IDM=1

'load_surf'

Surface_load_geom_ass IDM=1

* Load_case_control_data

! ---------------------------------

Loadcases IDM=2

1 2

Active_load_flags IDM=2

2 2

! ------------------------------------

! History data

! ------------------------------------

* History_point NUM=1

! ------------------------------------

Name "center"

Group 1

Output_frequency_increment 5

Point_coordinates IDM=3 JDM=1

0.0 0.0 0.0

Element_data IDM=1

"ELT_PORE"

Nodal_pore_pressure IDM=1

Pore_nod

! ------------------------------------

! Damping data

! ------------------------------------

* Damping_global_data

! --------------------------------------

Percentage_damping 0.02000

Bulk_damping_model "BulkViscosity"

Bulk_damping_properties IDM=1

0.500000

! ======================================

! Control Stage data

! ======================================

* Time_scaling_factors

! --------------------------------------

Optimal_time_step 1E-2

* Control_data

! --------------------------------------

! General setup

Control_title "Stage1"

Solution_algorithm 7

! Coupled incremental data (Flow step)

Maximum_number_time_steps 1E8

Duration 111

Initial_time_increment 1E-2

! Geomechanical iteration data

Maximum_number_iterations 5000

Factor_critical_time_step 0.9

! Tolerance

Displacement_norm_tolerance 0.01

! Output Data

Output_time_plotfile 1.00

Screen_message_frequency 100

Output_frequency_plotfile -1

Output_frequency_restart -1

1Mandel geometry file is imported after generated and converted from Gmsh into ParaGeo-compatible format.

2Geometry sets for each surfaces are set, followed by the volume.

3Element_type is set to HEX8, indicating the use of hexahedral element. By default, Bbar formulation is used when implicit geomechanical solver is chosen below. Porous_flow_type is set to 4 (coupled).

4Material and fluid properties are defined

5The displacement is fixed in the whole volume during initialisation stage.

6The volume is to be prescribed with pore pressure during initialisation stage.

7A pore pressure of 0.001 MPa is prescribed within the volume following the Time_curve_data NUM=1

8Damping data is defined.

9Incremental fixed stress coupling algorithm is used. The volume update model is set to Variable_group.

10Control data for initialisation stage is set. In particular, we choose Solution_algorithm as 7, indicating the use of implicit geomechanical solver.

11Boundary conditions are reset for stage 2 loading. All surfaces connected to interior region of sphere are prescribed with symmetry boundary conditions. The pore pressure on the outer surface of the sphere is to be prescribed.

12The outer surface is prescribed with zero pore pressure to allow drainage by following the Time_curve_data NUM=1.

13The external load is instantaneously applied on the outer surface at the same time as the interstitial fluid is allowed to drain on the same surface.

14History output of pore pressure at the center of the sphere is setup.

15Control data for loading stage is setup.

Results

The result files for the project are in directory: ParaGeo Examples\Validation\Val_002\Results. History results are plotted into Val_002b.xlsm sheet. Users can also generate analytical solution from the sheet as well.

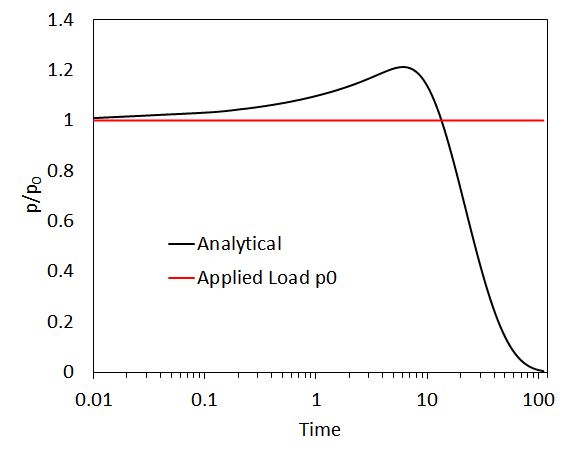
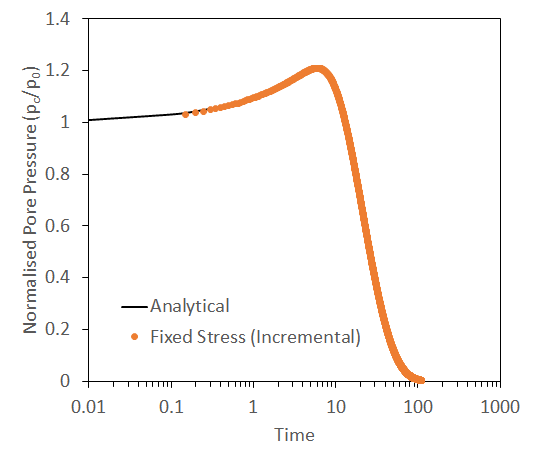
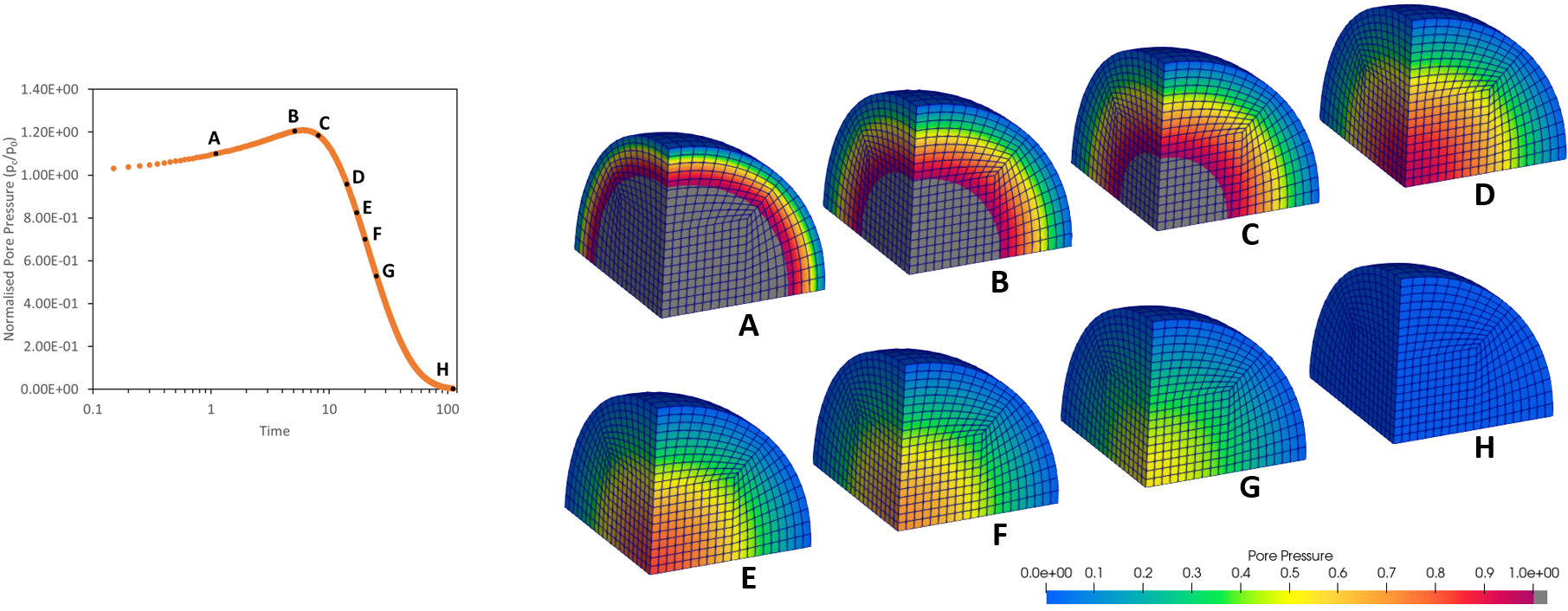
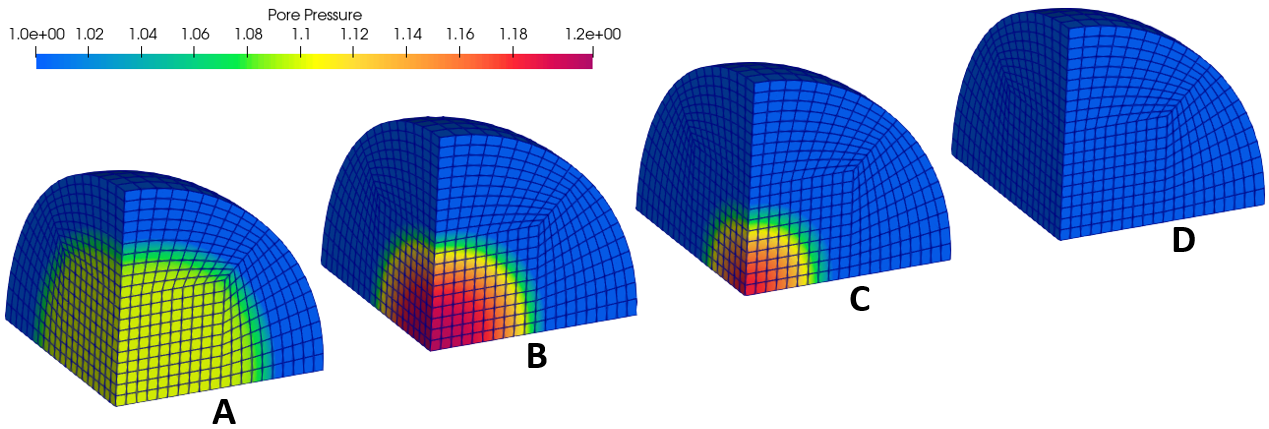
The gray part in the center represents the overpressure region (i.e., pc/p0 > 1.0), which is generated because the interstitial fluid cannot escape in time due to permeability and distance to the drainage boundary. Over time, the overpressure region will reduce in size, but the overpressure level will experience momentary peak at the center before dropping to zero. Overall, the numerical solution compares well with the analytical prediction of Mandel-Cryer effect.

Val_02b_04

Mandel-Cryer effect. Evolution of pore pressure within soil sample as a result of constant load applied instantaneously. Numerical solution agrees well with the analytical solution.

Val_02b_05

Evolution of pore pressure (Gray part representing overpressure region)

Val_02b_06

Evolution of overpressure. While the overpressure region subsides in size, the overpressure value at the center increases momentarily before decreasing.

References

[1] Cryer, C. (1963). A comparison of the three-dimensional consolidation theories of Biot and Terzaghi. Quart. J. Mech. and Appl. Math, 16, 401-412.

[2] Gibson, R., Knight, K., & Taylor, P. (1963). A critical experiment to examine theories of three-dimensional consolidation. Proc. Eur. Conf. Soil Mech. Wiesbaden, 1, 69-76.

[3] Leeuw, E. D. (1965). The theory of three-dimensional consolidation applied to cylindrical bodies. Proc. 6th Int. Conf. Soil Mech. and Found. Engng, 1, 287-290.

[4] Mandel, J. (1953). Consolidation des Sols. Geotechnique, 7, 287-299.

[5] Verruijt, A. (1965). Discussion on consolidation of a massive sphere. Proc. 6th Int. Conf. Soil Mech. Montreal, 3, 401-402.

[6] Verruijt, A. (2008). Consolidation of soils. In Encyclopedia of Hydrological Sciences. Chichester, UK: John Wiley & Sons, Ltd.