Case01 von Mises
Case 01 is based on the von-Mises elasto-plastic model with properties defined as:
|
||||||||||
von Mises Material Properties |
Following are descriptions of some key data and the element types investigated for the implicit and explicit analyses.
Material_data
Material_data defines the material properties of the model.
|
Group_data
Group_data sets the group name, element type, material name, porous flow type and the associated volume entity.
|
Results
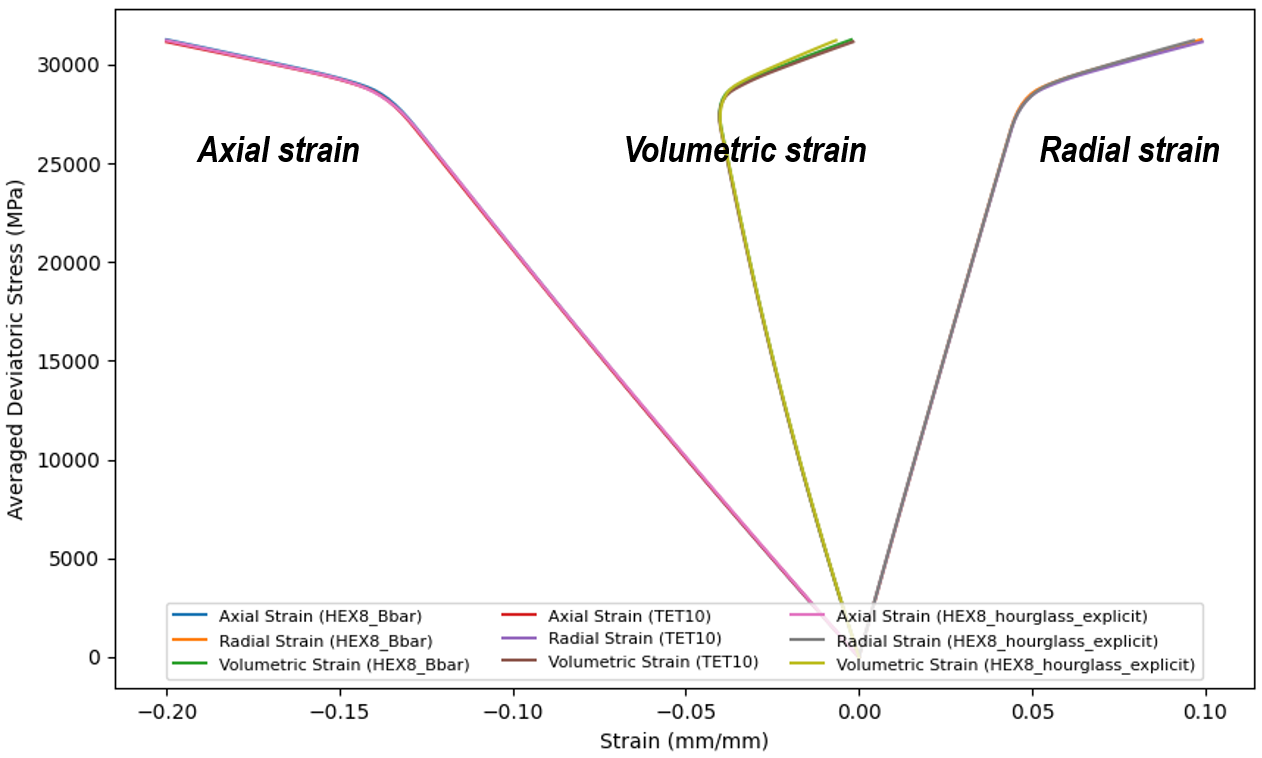
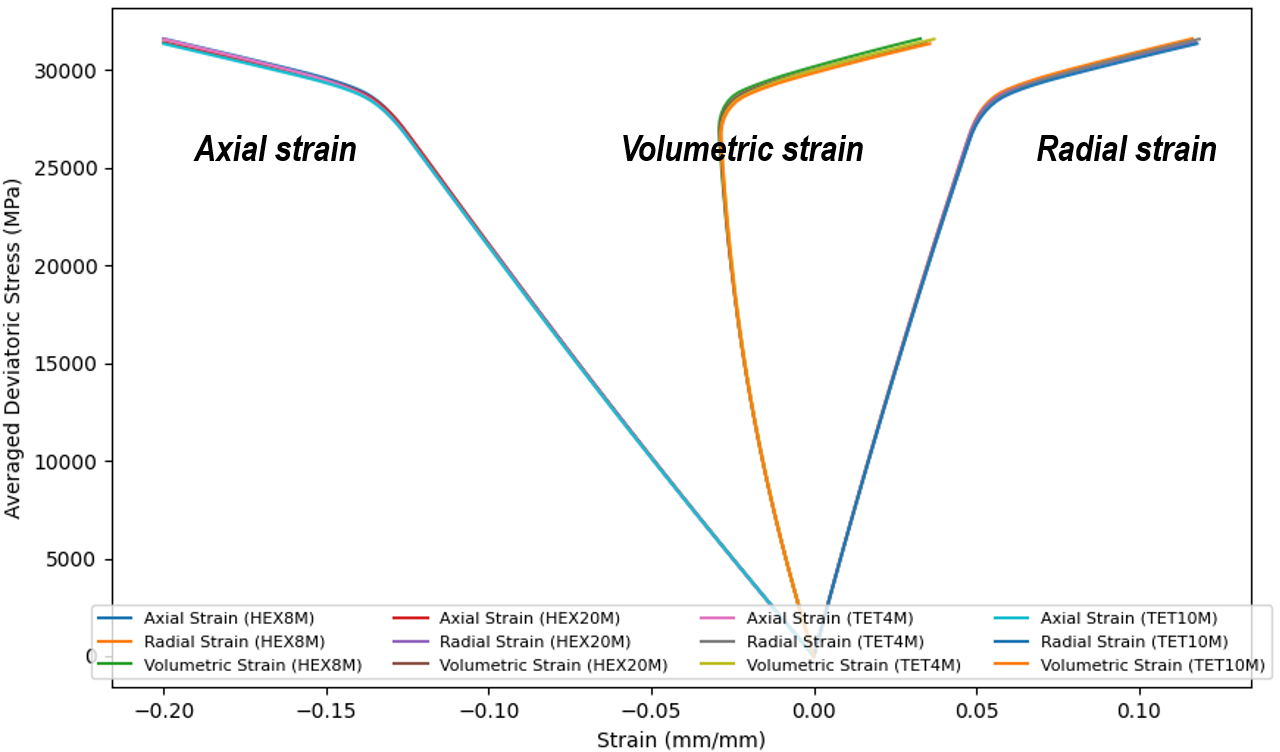
The following figures show the development of axial, volumetric and radial strains in terms of averaged deviatoric stress. The latter is computed as the average of the whole billet. As the compression load increases, axial strain increases in negative value while the radial strain increases in the positive value due to Poisson’s effect. When the stress state reaches the von-Mises yield surface, both strain parameters increases sub-linearly. Volumetric strain is computed as εvol = εaxial + 2εradial.
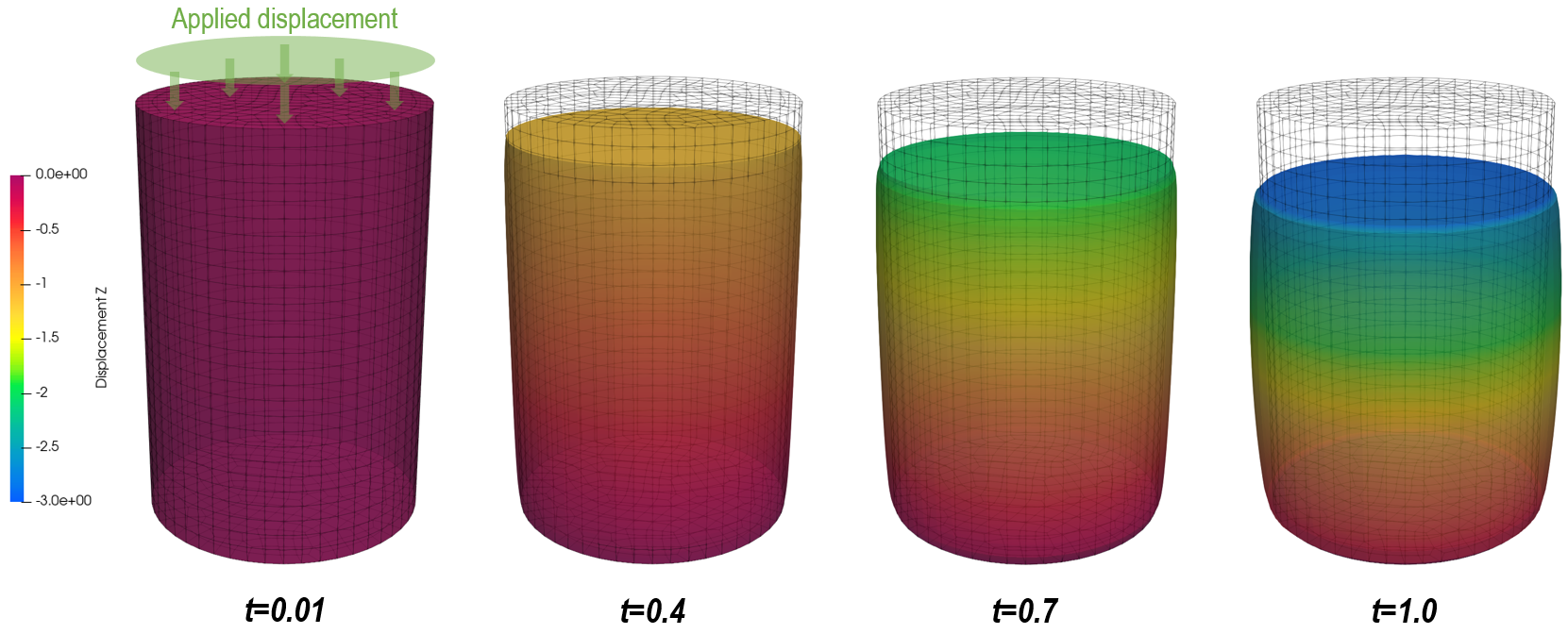
Billet compression as the applied displacement increases
We observe volumetric compression during elastic stage because the effect of axial strain is more dominant. In plastic stage, however, the contribution of radial strain to the volumetric strain has become more dominant, and thus we observe volumetric expansion. This trend would lead to plastic collapse if the compression load continues further.
Development of axial, volumetric and radial strains in terms of averaged deviatoric stress for standard elements
Development of axial, volumetric and radial strains in terms of averaged deviatoric stress for elements with mixed formulation
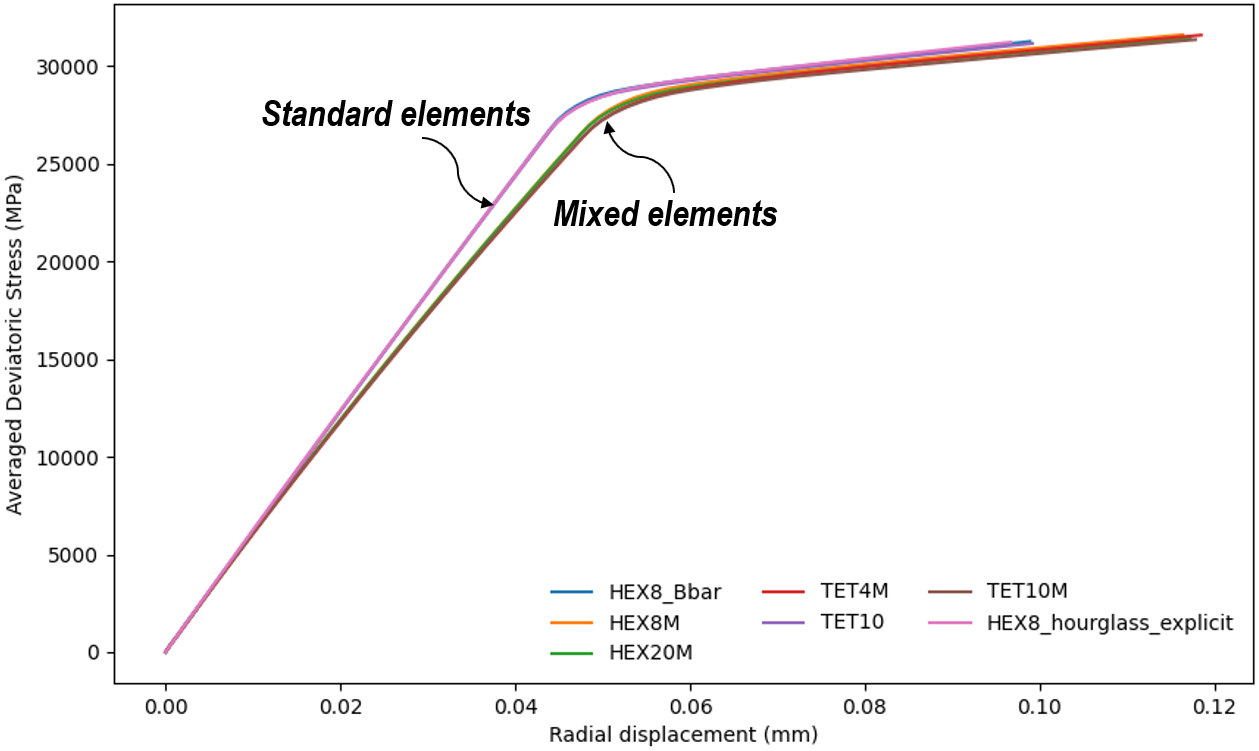
The figures above are separated by the standard element group and the mixed element group mainly to ease visualisation, lest legend be overloaded by the labels. It should be mentioned that the plot of strain parameters differ slightly between the standard and mixed element groups. This difference is also highlighted in the figures where the averaged mean stress and the averaged deviatoric stress are plotted against radial displacement. Compared to the standard elements, mixed elements exhibit smaller increase in stress for each increment of radial displacement. It is expected that elements associated with mixed formulation can alleviate the averaged mean stress better than the displacement-based elements.
Averaged mean stress plotted against radial displacement
Averaged deviatoric stress plotted against radial displacement
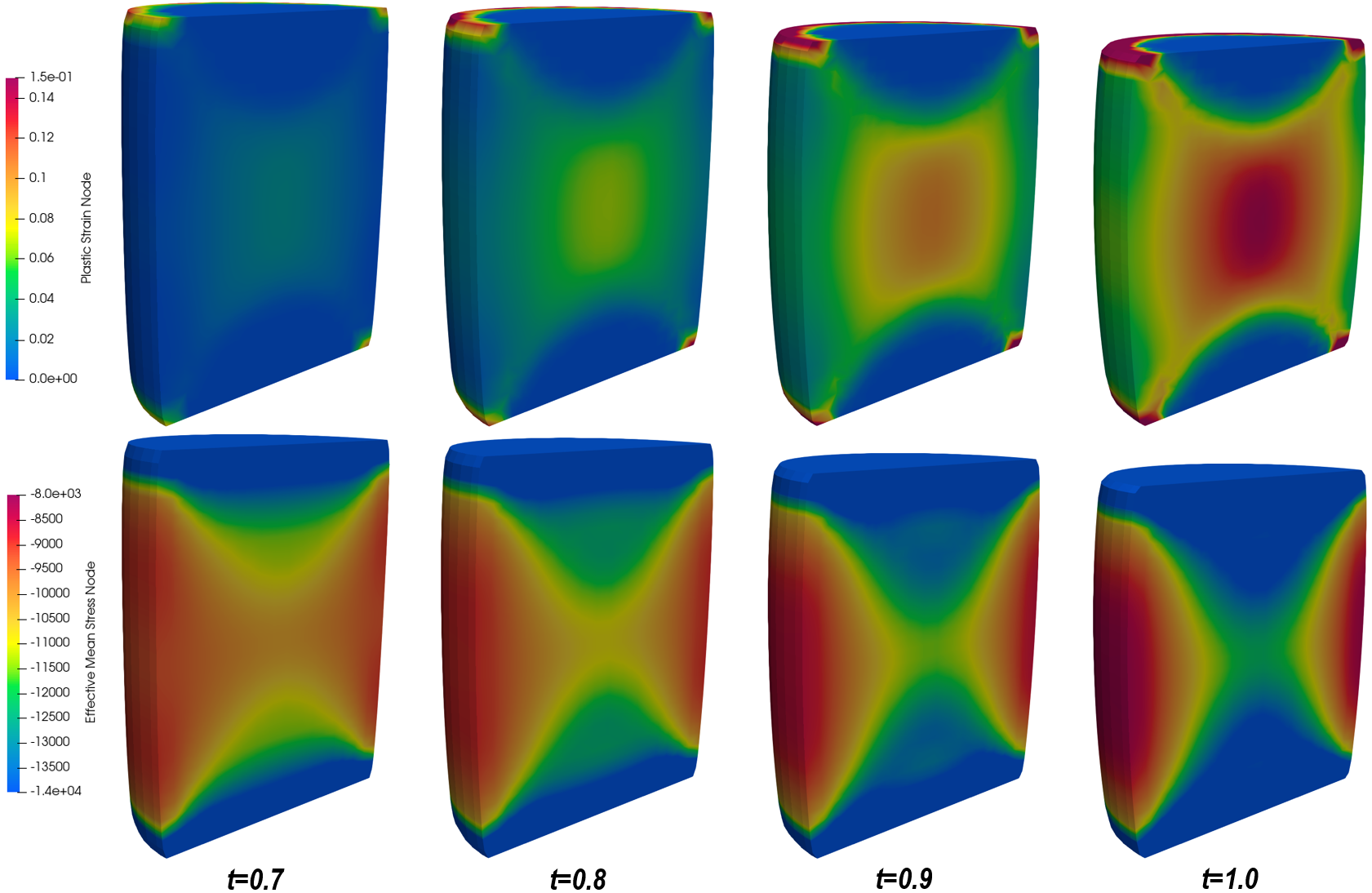
The plastic strain and effective mean stress evolution as shown in the figure below is driven by the concurrency of both axial and radial strain development. The difference between the axial and radial stress results in distortional (shape-changing) deformation within the billet. This is reflected by the plastic strain. As the circumferential surface of the billet is progressively displaced sideways, the effective mean stress is observed to increase and also become gradually concentrated towards the lateral surface, signifying the imminence of plastic collapse.
Development of plastic strain and effective mean stress on HEX8M model in clipped view
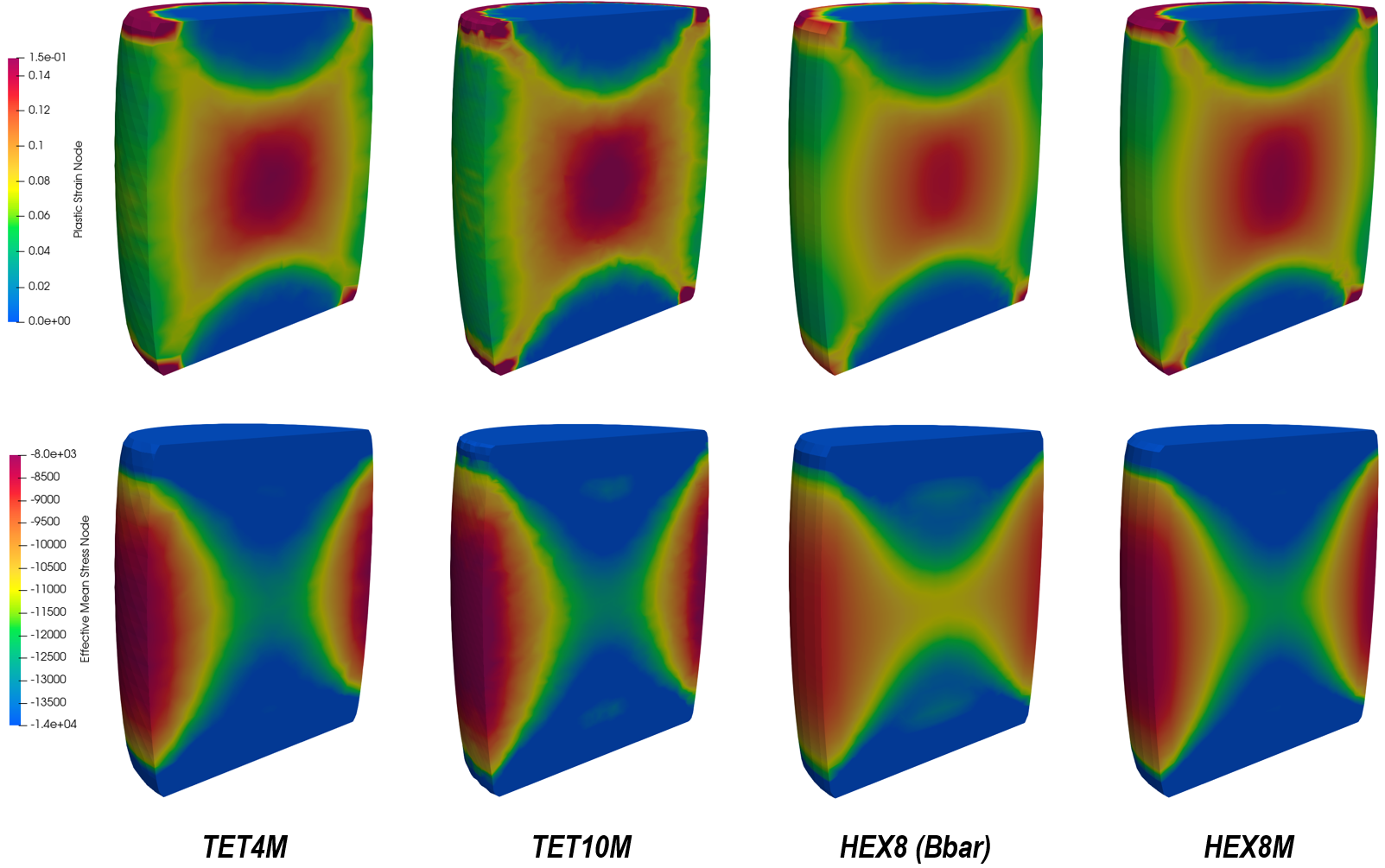
Comparison of plastic strain and effective mean stress distribution at final time step for different element types in clipped view
|
References
[1] Lippmann, H. (1979). Metal Forming Plasticity. Springer-Verlag, Berlin. [2] Cheng., J.H., Kikuchi, N. (1984). An analysis of metal forming processes using large deformation elastic-plastic formulations [3] https://abaqus-docs.mit.edu/2017/English/SIMACAEEXARefMap/simaexa-c-rezonebillet.htm
|