The data file for this exercise is located in directory: mech_001\Exercises\Case1D\Data. Look for ! TODO  text in the datafile and follow the instructions.

 

A small amount of high frequency damping is applied by default in the mechanical field; i.e. using a algorithm similar to the shock-wave smoothing algorithms used in hydrocodes.    In quasi-static problems, however, it can be advantageous to apply additional damping to gradually diminish the dynamic response of the system.  This can be achieved by defining either:

 

1Damping_global_data - which applies damping to the complete problem domain.

 

2Damping_nodal_data - which allows different levels of damping to be assigned to specific geometry entities defining the problem domain.

 

In both cases percentage damping is defined  based on an estimated value of the lowest vibration frequency computed using the Rayleigh quotient.  Generally percentage damping is specified in the range 0.01 - 0.03 (1% - 3%) as larger values of damping may result in significant over-damping which is generally detrimental to the solution.  In this case Damping_global_data is used to apply 2% percentage damping to the complete domain.

 

 

 

 

The results are visualized by plotting the high definition history data for global energy and points output in files mech_001_2d_Case1d_000.hdh and mech_001_2d_Case1d_001.hdh respectively.

 

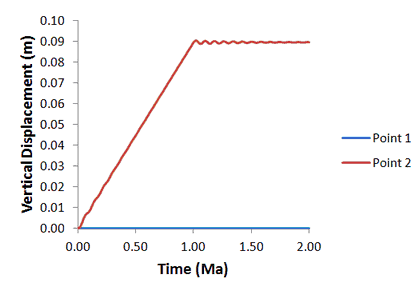
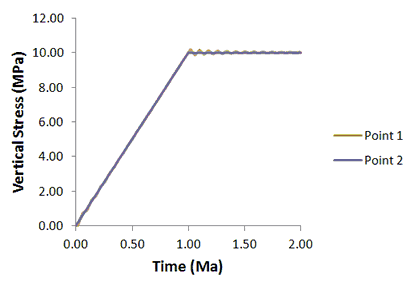
The time history for displacement and stress show that damping reduces the peak magnitude of the oscillations and eventually eliminates the dynamic response leading to a quasi-static stress state.  In achieving this state, however, there is still a small overshoot in stress at time t=1.0.   In an elastic simulation this is not significant.  In a nonlinear simulation, however, this could lead to a small additional non-recoverable deformation and is therefore not desirable.

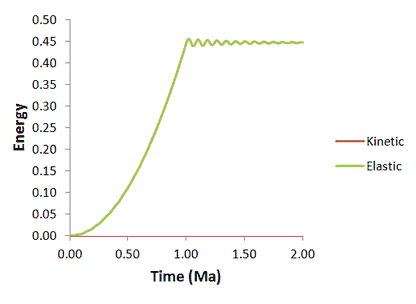
Damping of the dynamic response is also evident in the time history of elastic energy