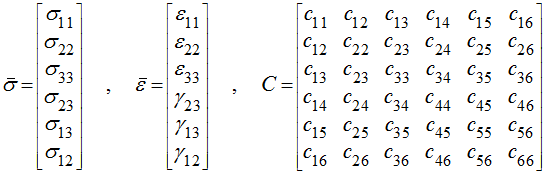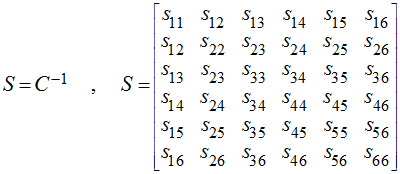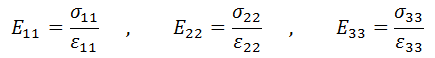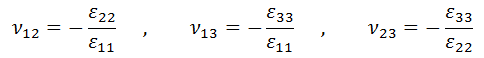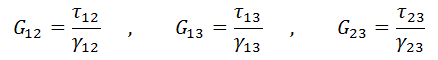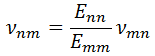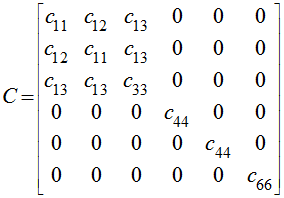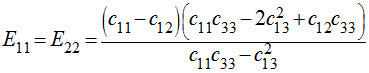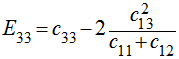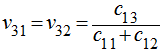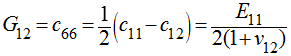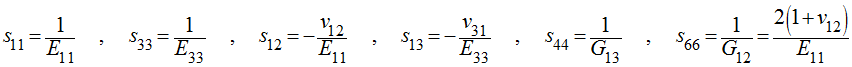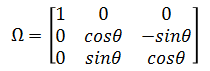Ex_003 Transverse Isotropic Elasticity

In this example a single 3D element is subjected to triaxial test conditions. For simplicity the model geometry has been defined as a cube of 1 m x 1 m x 1 m. The material characterization considers transverse isotropic elasticity with the axis of symmetry being the material axis x3. Note that the convention adopted is that the axes of the material coordinate system will be refereed as x1, x2 and x3 whereas the global coordinate axes will be referred as x, y and z. Several simulations will be performed with different material coordinate system rotations along the x axis. The simulations will consider a confining pressure load on planes perpendicular to x and y axes of 10.3 MPa and a displacement load aligned with the z axis corresponding to 1% of strain. The results from the simulations will be compared to the analytical solution when the axial stress reaches a magnitude of 140 MPa. The transverse isotropic material properties will be:

 

E11 = 30000 MPa

E33 = 15000 MPa

ν12 = 0.270

ν31 = 0.225

G13 = 7500 MPa

 

And from those we can derive:

 

G12 = 11811 MPa

ν23 = 0.450

 

hmtoggle_plus1The theory for the derivation of the material parameters is shown here.

Hooke's law can be expressed in tensorial form as:

 

 

where:

 

 

The inverse of the Hooke's law can be expressed as:

 

 

where:

 

 

 

For an orthotropic symmetry the anisotropic elastic properties can be expressed in terms of the Young's modulus, Poisson's ratio and shear modulus on each direction. Those are:

 

Where are the Young's modulus, normal stress and axial strain in the direction respectively, is the Shear modulus in the , plane, is the shear stress in the , plane aligned with axis and is the Poisson's ratio expressing the strain along axis due to the strain along axis.

 

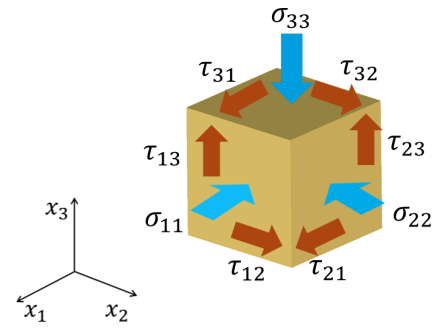
Due to symmetry in stress and strain tensors and given the symmetries involved in an orthotropic material, .

 

 

 

Ex_003_04

Schematic of stresses and strains aligned with the material coordinate system

 

 

 

 

For a transverse isotropic (TI) material in which the axis of symmetry is parallel to axis 3, the stiffness matrix can be written as:

 

 

where there are five independent parameters , , , and as .

 

The compliance matrix (= ) for a TI material can be written as:

 

 

For TI materials the equivalence between the stiffness parameters and the engineering constants is as follows:

 

 

 

 

 

 

 

 

And the equivalence between the compliance parameters and engineering constants is as follows:

 

 

 

 

Ex_003_01

Material coordinate system

 

 

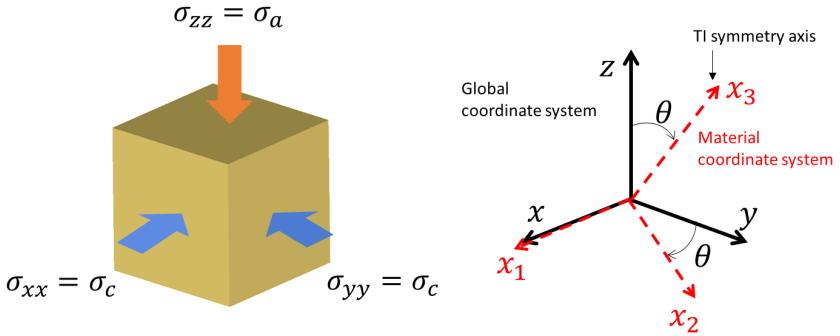
Ex_003_02

Schematic of problem boundary conditions

 

 

 

This example aims to be a reference for:

•Setting transverse isotropic elastic materials

•Assign rotations to the material coordinate system

 

The data files for the examples is found in: ParaGeo Examples\General Examples\Ex_003\Data

 

Note that the data files will be named according to the following convention: Ex_003a_15deg.dat where the last two digits before the file extension indicate the material system rotation along the x axis in degrees.

 

 

Material_data

Data File

 

 

* Material_data                          NUM=1

! -------------------------------------------------------------

 Name                          "Orthotropic"

! -------------------------------------------------------------

 Grain_stiffness                    34000.0     ! MPa

 Grain_density                       2650.0     ! kg/m3

! -------------------------------------------------------------

 Porosity_model_type                      1      

 Porosity                           0.20000      

! -------------------------------------------------------------

 Elastic_model_type                       3      

 Elastic_properties           IDM=9

  /"Young's modulus in X-direction"/      3.0000E+04     ! MPa

  /"Young's modulus in Y-direction"/      3.0000E+04     ! MPa

  /"Young's modulus in Z-direction"/      1.5000E+04     ! MPa

  /"Poisson's ratio in X-Y plane"/            0.2700

  /"Poisson's ratio in Y-Z plane"/            0.4500

  /"Poisson's ratio in Z-X plane"/            0.2250      

  /"Shear modulus in X-Y plane"/          1.1811E+04     ! MPa

  /"Shear modulus in Y-Z plane"/          7.5000E+03     ! MPa

  /"Shear modulus in Z-X plane"/          7.5000E+03     ! MPa    

! -------------------------------------------------------------

 Singlephase_fluid_name              "Water"

! -------------------------------------------------------------

 Permeability_type                            1      

 Permeability                        1.0000E-10 ! m2

! -------------------------------------------------------------

 Biot_type                                    1      

 Biot_constant                           1.0000

 

 

 

* Fluid_properties

! -------------------------------------------------------------

 Name                                "Water"

 Fluid_type                          "Water"

! -------------------------------------------------------------

 Stiffness                           2000.0     ! MPa

 Density                             1000.0     ! kg/m3

! -------------------------------------------------------------

 Viscosity_type                           1     ! Constant viscosity

 Viscosity                           1.00E-9   ! MPa*s

 

 

1.The material is named "Orthotropic"

2.Grain properties are defined.

3.Porosity_model_type is set to 1 (porosity is updated with strain)

4.Initial porosity (reference) is set to 0.2

5.Elastic_model_type is set to 3 (linear orthotropic elastic)

6.Nine elastic properties are provided to define the linear orthotropic model. In this case the properties are defined in such a way so that the model is transverse isotropic with the symmetry axis aligned with z direction. The derivation of the material properties for a transversely isotropic material is shown in the results section.

7.Fluid named "Water" is assigned to the material.

8.Permeability_type is set to 1 (constant permeability).

9.Permeability value is set to 1·10-10 m2.

10. Biot_type is set to 1 (constant Biot parameter value)

11. Biot constant is set to 1.0

12. Fluid properties for water are defined (self explanatory)

 

 

 

Rotation on material system

Data File

 

 

* Coordinate_system   NUM=1

! ----------------------------------

 Name  "Mat_system"

!  15 degrees rotation around X axis

 Direction_cosines    IDM=3 JDM=3

   1.0000         0         0

        0    0.9659   -0.2588

        0    0.2588    0.9659

 

 

* Group_data          NUM=1

! --------------------------------------

 Group_name                "Rock"

 Element_type              "HEX8"

 Material_name             "Orthotropic"

 Material_system           "Mat_system"

 Volumes              IDM=1

 1

 Porous_flow_type          1 ! 1-porous (dry)

 

 

 

1.A Coordinate_system is defined in order to define the rotation of the material system.

2.The Coordinate_system is named "Mat_system"

3.The direction cosines corresponding to the rotation are defined. In this case a rotation of 15 degrees along the X axis is defined and the direction cosines matrix can be easily calculated as:

where is the angle of rotation (see the figure at the top of this manual page). In the International Society of Biomechanics web page an Excel Spreadsheet developed by Neil Crawford to calculate direction cosines for a X, Y, Z sequential 3D rotation can be downloaded. The instructions are included in the spreadsheet.

4.The coordinate system is assigned as a material system within Group_data structure. It has to be assigned using the Material_system keyword.

 

 

 

 

 

Results

The result files for the project are in directory: ParaGeo Examples\General Examples\Ex_003\Results.

 

 

 

 

 

Where and are the axial and confining stresses respectively.

 

 

 

 

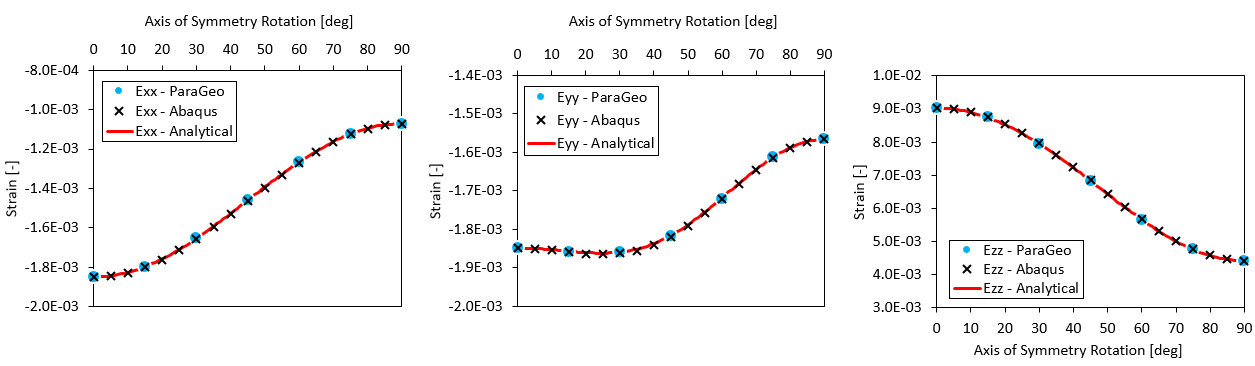
It can be seen that the simulation results match very well the analytical solution for the three strains for different amount of rotations.

 

 

Ex_003_03

Comparison of ParaGeo and Abaqus simulation results for strains in X, Y and Z directions with the corresponding analytical solutions