Superelements (SEs) are used to reduce very large models that will be simulated multiple times to smaller models, therefore increasing the total efficiency and allowing quicker design cycles or iterations in the analysis.

 

The principle used in SE analysis is often referred to as substructuring. That is, the model is divided into a series of components (SEs), each of which is processed independently, resulting in a set of reduced matrices that describe the behaviour of the SEs as seen by the rest of the structure. These reduced matrices for the individual SEs are combined to form an assembly (or residual) solution. The results of the assembly solution are then used to perform data recovery (calculation of displacements, stresses, etc.) for the SEs.

 

In static analysis, the theory used in SE processing is exact.

 

Efficiency is the primary reason to use SEs, and they are particularly advantageous in inverse modelling where a model must be solved many times during the inversion process. In ParaGeo the functionality is designed to allow creation and usage of a single SE that generally represents the linear elastic portion of the model.

 

The three operations that can be performed on a SE are;

1.‘Create’ – Create and write the SE to a file

2.‘Use’ – Read the SE file and perform a simulation using the SE

3.‘Reflate’ – Reflate the SE to provide results for the complete mesh

See later for further description of the SE operations.

 

A SE is defined by;

1.the element groups that will comprise the SE

2.the "retained freedoms" that will represent the SE after it has been constructed

 

The retained freedoms are the freedoms that remain and will be;

•boundary nodes to connect the SE with the remainder of the model (SE Class 1)

•nodes subjected to loading defined in the SE ‘use’ model and therefore must exist (SE Class 1)

•nodes required to compute target results in the SE ‘use’ model, e.g. the nodes associated with history point output (SE Class 2)

•couple freedoms master node in the SE ‘use’ model (SE Class 3)

 

 

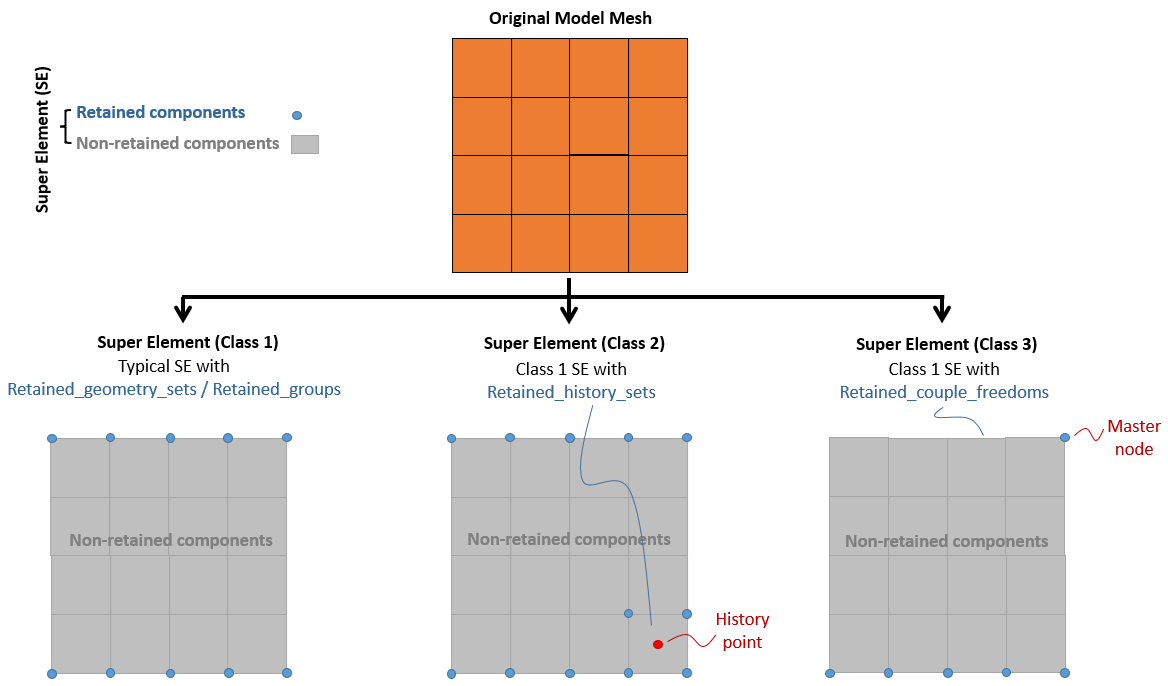
Illustration of Super Element (SE) concept and the 3 classes of SE

 

 

To ensure efficiency, the number of retained SE freedoms must be as low as possible.  In some cases where a constant load case (e.g. prescribed lateral displacement) is to be applied to the model, using coupled freedoms can be advantageous as it allows all the nodes that will be prescribed to be eliminated and represented with a single master node, thus greatly reducing the number of retained freedoms.

 

The retained, or exterior freedoms, are best described as those that are retained for further analysis or where the SE connects to the rest of the structure. Structural matrices are assembled for each SE, and the matrices go through reduction processing until the only remaining terms are for the retained freedoms. These reduced matrices are used to represent the properties of the SE when it is attached to the rest of the model.

 

Eliminated, or interior freedoms, are those that are condensed out during SE creation. The reduction process is generally known as static condensation.

 

SE creation

This step performs static condensation on the SE groups to form the SE defined by the retained freedoms.  This SE is then saved to a file with extension .suelmat for later use in the usage phase. Creation of the SE is CPU and Memory intensive and is generally more expensive in terms of CPU than solving the standard model for large problems.

 

The SE creation operation can be performed in parallel in the following manner;

1. The model is automatically sub-divided into domains

2. A SE is computed for each domain sequentially (several domains may be computed at the same time if there is sufficient CPU and Memory resource).

3. The domain SEs are progressively "merged" until either a single or specified number of SEs remain. This operation requires further static condensation of the shared boundary nodes that are not retained.

 

SE usage

The SE, in conjunction with other retained element groups, is solved to evaluate the solution for the reduced problem. Generally this operation will be performed multiple times.

 

SE reflation

During this step, the solution for the reduced problem is used to evaluate the solution of the complete model.  The CPU cost of this step is similar to the cost of solving a single model. In an optimisation procedure, this is only performed on a single or a few of the most optimal models.

 

 

 

Examples

 

Suggested tutorial examples demonstrating usage of super element in ParaGeo are:

 

SuEl_001: Super Element Workflow

 

MEM_003: Boundary Optimisation and Super Element