Case5 Usage of Spatial Plan (lateral variations in properties)
The data files for the project are in directory: SpatVar_001\Exercises\Case 5\Data. Look for ! TODO text in the datafile and follow the instructions.
This tutorial exercise assumes that Case4 is previously completed. In this exercise the Grid from Case 1 will be used to initialize porosity. A spatial plan (Spatial_grid type Plan1) will be used to define a lateral change in facies by assigning a facies factor. Then spatial_table is going to be used to assign Young's modulus and Poisson's ratio as a function of facies. To perform this exercise modify the data as shown bellow. Grid and spatial table data can be copied from excel file "SpatVar_001_case5.xlsx" .
Include
Data File |
|
* Include ! --------------------------------- Filename "porosity_SpatVar_001_case5.spat"
|
1The included file name should point to the edited .spat file (ending with suffix _case4).
|
Spatial_grid
Data File |
|
* Spatial_grid NUM=1 ! ---------------------------------------- Name "Porosity_Spatial" Type "Grid1" Num_cells_x 10 Num_cells_y 4 Num_cells_z 8 Cell_division_X 800 Cell_division_Y 1000 Cell_division_Z 500 Grid_origin IDM=3 0.0 0.0 0.0 Nodal_variables IDM=2 "Porosity" "P_strnv"" Point_values IDM=2 JDM=495 0.05 -0.553652881 0.049 -0.554013553 . . . 0.390672 -0.159889195
|
1The grid definition is identical to case 1 |
Spatial_plan
Data File |
|
* Spatial_grid NUM=2 ! ---------------------------------------- Name "Facies_Spatial" Type "Plan1" Num_division_x 8 Num_division_y 4 Plan_variables IDM=1 "Facies" Plan_points IDM=2 JDM=45 0 0 1000 0 . . . 8000 4000 Plan_values IDM=1 JDM=45 0.0 0.125 . . . 1.0
|
1A second grid is defined in the file "porosity_SpatVar_001_case5.spat" in order to define the facies factor. 2The Type is set to Plan1 3Eight divisions are going to be considered in X direction and four divisions in Y direction (1000 m long each). 4The plan variable is named as "Facies" (arbitrary name). 5Plan_points coordinates are defined with regular separation of 1000m in X and 1000m in Y. 6In Plan_values the facies factor is assigned. In this example for a given X the facies factor is constant in Y. The facies factor varies linearly from 0 in X=0 to 1 in X=8000. |
Spatial_state_set
Data File |
|
* Spatial_state_set NUM=2 ! --------------------------------- Spatial_grid "Facies_Spatial" State_variables IDM=1 "Facies"
|
1A second spatial_state_set is defined to assign the "Facies" variable (facies factor) |
Spatial_table
Data File |
|
|||||||||
* Spatial_table NUM=1 ! --------------------------------- Material_names IDM=1 "Shale_CF75" Variable_name "Young" Dependent_variables IDM=1 "Facies" Dependent_grids IDM=1 "Facies_Spatial" Table_size IDM=1 2 Table_values IDM=2 JDM=2 20000 0.0 10000 1.0
* Spatial_table NUM=2 ! --------------------------------- Material_names IDM=1 "Shale_CF75" Variable_name "Poiss" Dependent_variables IDM=1 "Facies" Dependent_grids IDM=1 "Facies_Spatial" Table_size IDM=1 2 Table_values IDM=2 JDM=2 0.22 0.0 0.35 1.0
|
1Two spatial_table data structures are defined, one to define Young's modulus as a function of facies and one to define Poisson's ratio as a function of facies. 2The only dependent variable in both tables is set to be "Facies" defined in the "Facies_spatial" spatial grid. 3In this example a facies factor of 1.0 corresponds to pure shale whereas a facies factor of 0.0 corresponds to pure sandstone. Properties for pure lithologies are provided as follows with assumed lineal variation for mixed lithologies:
4The values specified above are input through tables with size 2 for each variable.
|
Results
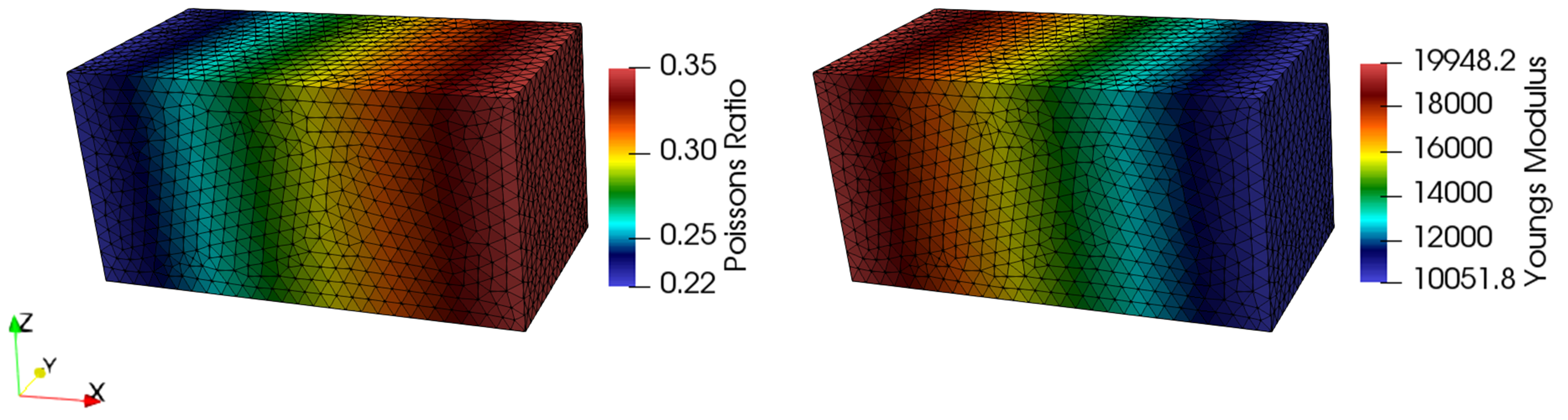
The result files for the project are in directory: SpatVar_001\Case5\Results. It can be observed that both Young's Modulus and Poisson's Ratio contours show a linear distribution in X direction according to the defined facies distribution.
Poisson's ratio (left) and Young's modulus (right) which are a function of the defined facies factor.
|