Case01 Ubiquitous Upscaled Fracture (UUF)
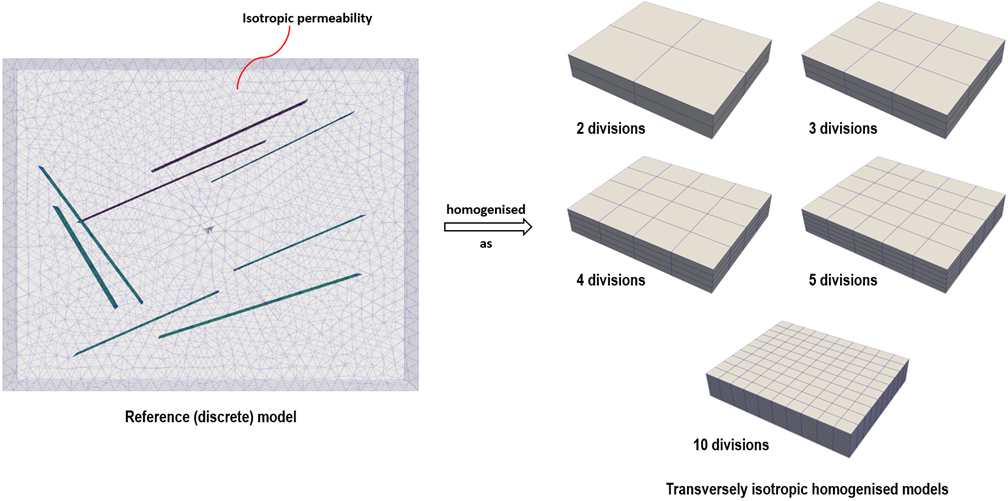
In the reference (discrete) model, the fractures are inserted as discrete surfaces into the matrix medium, which assumes isotropic permeability. In this example, the influence of these fractures on the flow field is then accounted for by including the effect of the fracture permeability in an upscaled homogenised transversely isotropic matrix permeability. Note that the homogenised model inherits the boundary conditions from the reference model. Five homogenised models with different number of divisions on all sides are simulated.
|
Fig. 1 Five homogenised models with different number of divisions on all sides are simulated. |
The starting folder structure with the data required for the inverse analysis is provided in Fract_004\Case01\Data and is as follows:
•Fract_004_case01.inp: Data file defining the inverse analysis to be run with the ParaGeoInv executable. •Target: folder containing the target results file(s) from Fract_002 to be used for optimisation. ▪fract_002_gen_exp_001.hdh ▪fract_002_gen_exp_002.hdh •Template: folder containing the template data file for homogenised model with 4 divisions that will be used to define all model simulation data files. ▪Fract_004_case01.dat •Test: "Empty" folder to which the simulation results will be written to.
To run the inverse analysis: 1.Create a Results folder in Fract_004\Case01 2.Copy all the files and sub-folders from the Data folder into the Results folder 3.Create an "empty" Test folder 4.Run the simulation in the Results folder by typing "parageoinv Fract_004_case01.inp" in a command prompt window. This will populate the "empty" Test folder with the simulation results. The .ParOpt, .ParBest and .ParAll files will be written to the main Results folder.
Note that to run the other homogenised models with a different number of divisions (as shown in Figure 1 above), change the template data file accordingly for the required number of mesh divisions and repeat the inverse analysis (see description of Structured_mesh_data below).
The optimisation variables for this inverse problem is permeability in x and y directions, namely kx and ky. We create placeholders for these variables in the ParaGeo template data file under Material_data data structure after the keywords Permeability_x and Permeability_y. The placeholders are denoted, respectively, by <p>Perm_x<p> and <p>Perm_y<p>.
In the following, we describe the setup of ParaGeoInv data file (Fract_004_case01.inp), which includes: 1Parameter_data defines the minimum and maximum, as well as the initial values of selected optimisation variables. 2NA_options tunes the parameters of optimisation algorithm, including tolerance, number of iterations, etc. 3Misfit_data_set defines the file name(s) of target solution and the variable name(s) to be compared with.
Also described is the Structured_mesh_data in the template data file (Fract_004_case01.dat) defining the number of mesh divisions utilised.
Note that only key data structures are described below. |
Parameter_data defines the minimum and maximum, as well as the initial values of selected optimisation variables.
|
NA_options tunes the parameters of optimisation algorithm, including tolerance, number of iterations, etc.
|
Misfit_data_set sets the file name(s) of target solution and the variable name(s) to be compared with.
|
Structure_mesh_data defines the number of mesh divisions via Default_divisions in the template data file Fract_004_case01.dat. This number is changed accordingly to run homogenised models with different number of divisions as shown in Figure 1 and results presented in Figure 2.
|
The result files for this example is available in directory: Fract_004\Case01\Results.
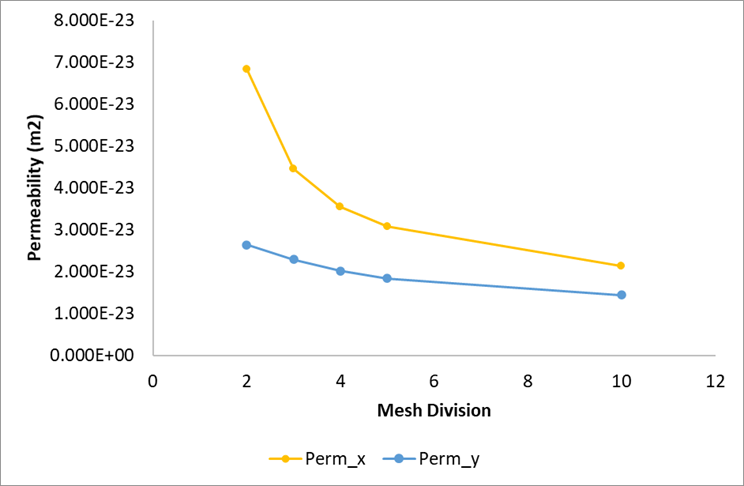
For the 4-division homogenised model, the optimal model achieved through inverse analysis corresponds to model number 182 (see fract_004_case01.ParOpt). Comparing against the reference discrete model whose matrix permeability (isotropic) is 1E-23m2, the fracture permeability in the homogenised model is perm_x = 3.543E-23m2 and perm_y = 2.082E-23m2.
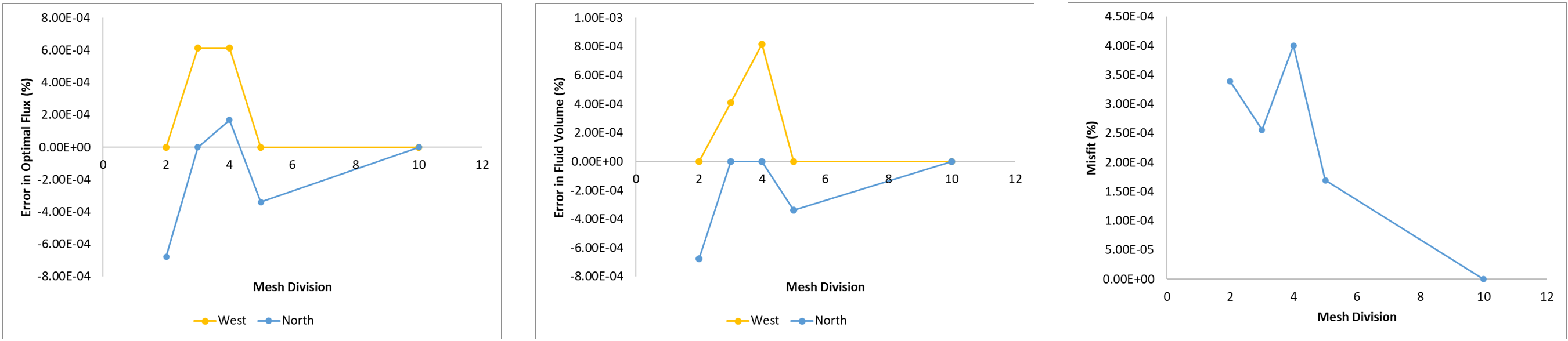
The following table shows the comparison of fluid volume and flow rate on the outlet surfaces between optimal values achieved through the ParaGeoInv algorithm for the 4-division homogenised model and the target values. Almost exact results are observed.
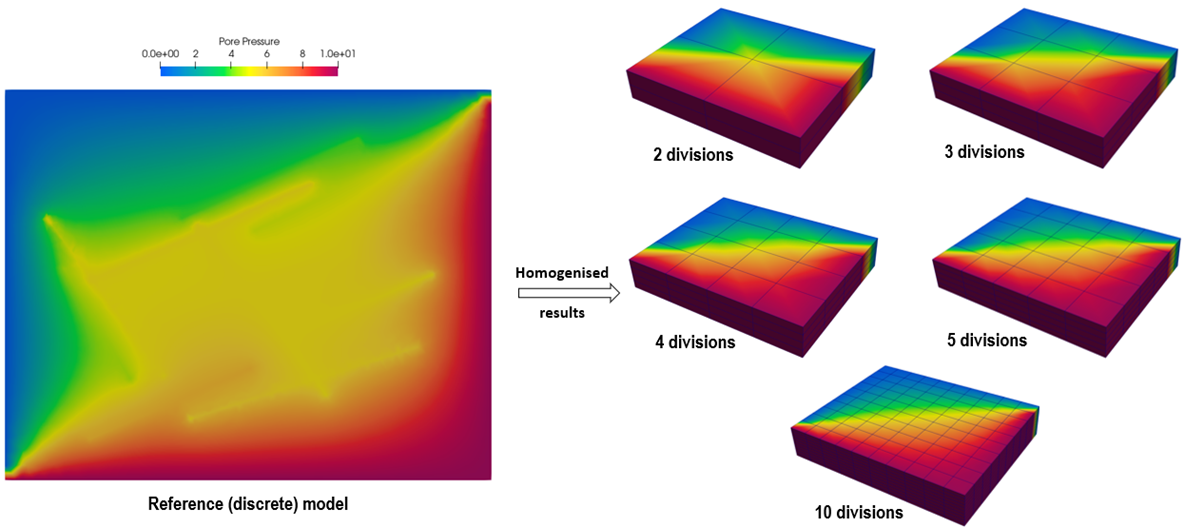
Figures 2 - Figures 4 show the results for the homogenised models with different number of mesh divisions. Optimal results of all homogenised models are obtained with low error, regardless of mesh size. The effect of mesh size is reflected in the change of effective permeability in both directions. Smaller mesh size accounts for higher pressure gradient, and thus lower permeability in both directions to maintain the mass flux. Using Darcy’s law, permeability can be approximated as being proportional to the inverse of element size.
|