Case01 Base Case

Contents

Following is the description of the data file for the project which is located in Imp_001/Case01/Data. Note that the data is not described in the same order as it appears in the data file but in an order that facilitates understanding of the model set up instead (i.e. geometry first, then mesh, then groups, etc.).

Also note that usage of the implicit solver for the geomechanical field is defined in Control_data exclusively whereas the rest of the data is common to an explicit case. Thus the present data file description is divided in two sections; first one defining the problem definition data and the second one defining Control_data set up for the implicit solver.

Geometry

The geometry of the model is defined towards the end of the data file after the END DATA command.

Data File

* nodal_data

! ----------------------

node_number IDM=20

1 2 ... 20

coordinates IDM=3 JDM=20

100.0 0.0 0.0

92.38795 38.26834 0.0

(...)

0.0 200.0 10.0

* geometry_volume NUM=1

! ----------------------

surfaces IDM=6

1 5 6 8 10 3

* geometry_volume NUM=2

! ----------------------

surfaces IDM=6

2 6 7 9 11 4

* geometry_surface NUM=1

! ----------------------

lines IDM=4

5 3 6 1

* geometry_surface NUM=2

! ----------------------

lines IDM=4

6 4 7 2

(...)

* geometry_surface NUM=11

! ----------------------

lines IDM=4

11 19 20 4

* geometry_line NUM=1

! ----------------------

points IDM=3

1 2 3

* geometry_line NUM=2

! ----------------------

points IDM=3

3 4 5

(...)

* geometry_line NUM=20

! ----------------------

points IDM=2

10 20

1.The 3D geometry is defined via:

▪20 nodes

▪20 lines

▪11 surfaces

▪2 volumes

2.Some of the Geometry_line are quadratic lines defined by three points.

Geometry sets

Data File

* Geometry_set NUM=1

! -----------------------

Name "Inn_surf"

Surfaces IDM=2

8 9

* Geometry_set NUM=2

! -----------------------

Name "Ext_surf"

Surfaces IDM=2

10 11

* Geometry_set NUM=3

! -----------------------

Name "SymY_surf"

Surfaces IDM=1

* Geometry_set NUM=4

! -----------------------

Name "SymX_surf"

Surfaces IDM=1

* Geometry_set NUM=5

! -----------------------

Name "OOP_surf"

Surfaces IDM=4

1 2 3 4

1.Five geometry sets are defined for:

▪Inner surface

▪External surface

▪Symmetry surface in the Y direction

▪Symmetry surface in the X direction

▪Out of plane surfaces (normal to Z axis)

Mesh

Data File

* Mesh_control_data

! ---------------------------------

Generation_algorithm 1

* Structured_mesh_data

! ---------------------------------

Default_divisions 5

Volumes IDM=2

1 2

List_structured_line_sets IDM=3

1 2 3

* Structured_line_set NUM=1

! ---------------------------------

Number_divisions 10

Lines IDM=2

1 2

* Structured_line_set NUM=2

! ---------------------------------

Number_divisions 20

Lines NUM=1

* Structured_line_set NUM=3

! ---------------------------------

Number_divisions 1

Lines IDM=1

1.Mesh data for discretizing the model into 400 structured hexahedral elements is defined.

Group data

Data File

* Group_control_data

! ----------------------------------------

Group_numbers IDM=1

Active_geomechanical_groups IDM=1

* Group_data NUM=1

! ----------------------------------------

Group_name "Sample"

Element_type "HEX8"

Material_name "VonMises"

Porous_flow_type 0

Volumes IDM=2

1 2

1.A single Group_data data structures is defined for the cylinder with:

a.Group name defined as "Sample"

b.Group defined with 8-noded 3D hexahedral elements

c.Material named "VonMises" is assigned to the group

d.Porous_flow_type is set to 0 (non-porous material)

e.The group is defined by volumes 1 and 2

Material data

Data File

* Material_data NUM=1

! =================================

Material_name "VonMises"

! ---------------------------------

Grain_density 1760

! ---------------------------------

Isotropic_elastic_properties IDM=2

/Young's Modulus/ 210000

/Poisson's Ratio/ 0.3

! ---------------------------------

Plastic_material_type 7

Plastic_properties IDM=1

/Yield Strength/ 240

1.A single material named "VonMises" is defined for the present case.

2.The material is defined a Young's modulus of 210 GPa and a Poisson's ratio of 0.3

3.Plastic_material_type is set to 7 which corresponds to von Mises plasticity.

4.Von Mises yield strength is defined as 240 MPa

Support data

Data File

* Support_data

! ----------------------------------------

Displacement_codes IDM=3 JDM=4

/Set1/ 1 0 0

/Set2/ 0 1 0

/Set3/ 0 0 1

/Set4/ 1 1 1

Displacement_code_geom_set IDM=3

"OOP_surf"

"SymX_surf"

"SymY_surf"

Displacement_code_geom_ass IDM=3

3 1 2

1.Displacements are constrained in the normal direction for the symmetry and out of plane surfaces.

Loading data

Loading data corresponding to the internal pressure is defined.

Data File

* Global_loads NUM=1

! ---------------------------------

Surface_load IDM=3 JDM=1

/Set 1/ 1.0 0.0 0.0

Surface_load_type 1

Surface_load_geom_set IDM=1

"Inn_surf"

Surface_load_geom_ass IDM=1

* Time_curve_data NUM=1

! ---------------------------------

Time_curve IDM=2

0.0 1.0

Load_factor IDM=2

0.0 200.0

Curve_type 1

* Load_case_control_data

! ---------------------------------

Loadcases IDM=1

Active_load_flags IDM=1

1.A Global_loads data structure to prescribe a normal surface load (Surface_load_type 1)is defined.

2.A load of 200 MPa is ramped up from time t=0 to t=1 following a linear ramp as specified in the Time_curve_data.

3.Load_case_control_data is defined to define the load as active.

History output

Data File

* History_point NUM=1

! -----------------------------------

Name "Corner"

Group 1

Output_frequency_increment 1

Point_coordinates IDM=3 JDM=1

200.0 0.0 10.0

Displacements IDM=1

"Disp_x"

1.A history point at the external surface is defined in order to output the radial displacement at each time increment.

Control data for the implicit solver

Usage of the implicit solver and the parameters defining the time increment, convergence criteria, etc is defined exclusively in Control_data.

Data File

* Control_data

! ============================================

Control_title "init"

Solution_algorithm 7

Initial_time_increment 0.1

Target_number_iterations 5

Maximum_number_iterations 12

Minimum_time_increment 0.0001

Maximum_time_increment 0.2

Maximum_number_time_steps 50

Displacement_norm_tolerance 0.01

Residual_norm_tolerance 0.01

Termination_time 1.0

Output_frequency_plotfile 1

Screen_message_frequency 1

1.Solution_algorithm set to 7 indicates usage of the implicit solver for the geomechanical field. If used then a convergence criteria must be specified which can be based on either or both:

a.Displacement_norm_tolerance (displacement based tolerance)

b.Residual_norm_tolerance (force based tolerance)

2.The Initial_time_increment indicates the initial time step for the explicit solver. Note that depending on the data specified in Control_data the time increment can be constant or variable during the simulation.

3.Specification of Target_number_iterations allows to use a variable time increment where its value can be increased above the initial one. If in previous time increments less iterations than the specified target were required top converge then the next time increment size will be multiplied by a factor of 1.25.

4.Maximum_number_iterations defines the maximum number of iterations for a given time increment to converge. If the maximum number of iterations is reached without convergence then the current time increment will be decreased by a factor of 2.

5.Minimum_time_increment indicates the minimum value allowed for the time increment. If convergence is compromised and a time increment lower than the specified value is required then the simulation will be terminated.

6.Maximum_time_increment imposes a maximum bound for the time increment even if convergence is achieved with less iterations than the target.

7.Maximum_number_time_steps imposes a maximum number of time increments to solve the current simulation stage which if reached simulation will be terminated (even if complete stage duration has not been performed).

8.Specification of Displacement_norm_tolerance defines convergence criteria based on the displacement norm. Then the input value (Dinp) establishes that the condition Dnorm ≤ Dinp must be satisfied where Dnorm is calculated as:

Where Δditer is the change in displacement increment at every iteration and Δdinc is the change in displacement for the current increment.

9.Specification of Residual_norm_tolerance defines convergence criteria based on the residual norm. Then the input value (Rinp) establishes that the condition Rnorm ≤ Rinp must be satisfied where Rnorm is calculated as:

Where Fmext is the external nodal forces for the geomechanical field and Fmint is the internal nodal forces for the geomechanical field.

10. Termination_time indicates the final time for the current simulation stage.

11.Output_frequency_plotfile set to 1 indicates that a plot file will be output every time increment.

12. Screen_message_frequency set to 1 indicates that simulation information will be printed on the command promt every time increment.

Results

The results for the project are located in Imp_001\Case01\Results.

Case01

The summary of step and convergence data printed both at the command prompt and the .res file is shown in the following table. In red is shown the data of the steps that did not converge. As can be seen at step number 3 the time increment increased above the initial one because in the previous two steps less iterations than the target were required (which means that the code is converging easily and thus larger time increments may be used). It can be noted that from step 5 onwards more than 2 iterations are required to converge as plastic strains start to develop from those steps.

Step num.	Time Increment	End Time	P (GPa)	Num. Iterations	Disp. Norm	Res. Norm
1	0.1	0.1	0.02	2	0.00	0.00
2	0.1	0.2	0.04	2	0.00	0.00
3	0.125	0.325	0.065	2	0.00	0.00
4	0.15625	0.48125	0.09625	2	0.00	0.00
5	0.19531	0.67656	0.135312	4	0.853E-4	0.00
6	0.19531	0.87187	0.174374	5	0.269E-2	0.00
7	0.12813	1.0	0.2	6	No conv.	No conv.
7	0.064063	0.93594	0.187188	2	100	0.155E+4

Summary of step and convergence results for Case01

Case01a

Case01a is set with the objective to obtain a solution for internal pressures of 0.1 GPa and 0.18 GPa respectively for which an analytical solution is provided in de Souza-Neto et al. (2008). Provided that the maximum internal pressure has been set to 0.2 GPa and the Time_curve_data has been set so that it is applied following a linear function from t=0 to t=1, the times corresponding to internal pressures of 0.1 GPa and 0.18 GPa are t=0.5 and t=0.9. Thus the Control_data for Case01a is set so that a constant time increment is used for the implicit solver as shown below.

Data File

* Control_data

! ============================================

Control_title "init"

Solution_algorithm 7

Initial_time_increment 0.05

Minimum_time_increment 0.01

Maximum_number_iterations 12

Maximum_number_time_steps 50

Displacement_norm_tolerance 0.01

Residual_norm_tolerance 0.01

Termination_time 1.0

Output_frequency_plotfile 1

Screen_message_frequency 1

1.Because Target_number_iterations is not defined the code will attempt to use a constant time increment of 0.05 as set in Initial_time_increment (the time increment will not increase but it may decrease if there are convergence difficulties).

The resulting time step and convergence data is summarized in the table below. The steps that did not converge are shown in red. The steps for which solution is compared to the analytical solution in de Souza-Neto et al. (2008) is shown in green. As can be seen, because Target_number_iterations was not set the time increment is kept at 0.05 even though the first 10 steps have converged with just two iterations. Note that from step 11 onwards more than 2 iterations are required as it is when plastic strains start to develop.

Step num.	Time Increment	End Time	P (GPa)	Num. Iterations	Disp. Norm	Res. Norm
1	0.05	0.05	0.01	2	0.00	0.00
2	0.05	0.1	0.02	2	0.00	0.00
3	0.05	0.15	0.03	2	0.00	0.00
4	0.05	0.2	0.04	2	0.00	0.00
5	0.05	0.25	0.05	2	0.00	0.00
6	0.05	0.3	0.06	2	0.00	0.00
7	0.05	0.35	0.07	2	0.00	0.00
8	0.05	0.4	0.08	2	0.00	0.00
9	0.05	0.45	0.09	2	0.00	0.00
10	0.05	0.50	0.10	2	0.00	0.00
11	0.05	0.55	0.11	4	0.705E-4	0.00
12	0.05	0.60	0.12	4	0.147E-3	0.00
13	0.05	0.65	0.13	4	0.990E-3	0.00
14	0.05	0.70	0.14	4	0.267E-4	0.00
15	0.05	0.75	0.15	5	0.469E-2	0.00
16	0.05	0.80	0.16	5	0.00	0.00
17	0.05	0.85	0.17	5	0.359E-4	0.00
18	0.05	0.90	0.18	5	0.935E-5	0.00
19	0.05	0.95	0.19	6	0.122E-2	0.00
20	0.05	1.00	0.20	6	No conv.	No conv.
20	0.025	0.975	0.195	1	100	65

Summary of step and convergence results for Case01a

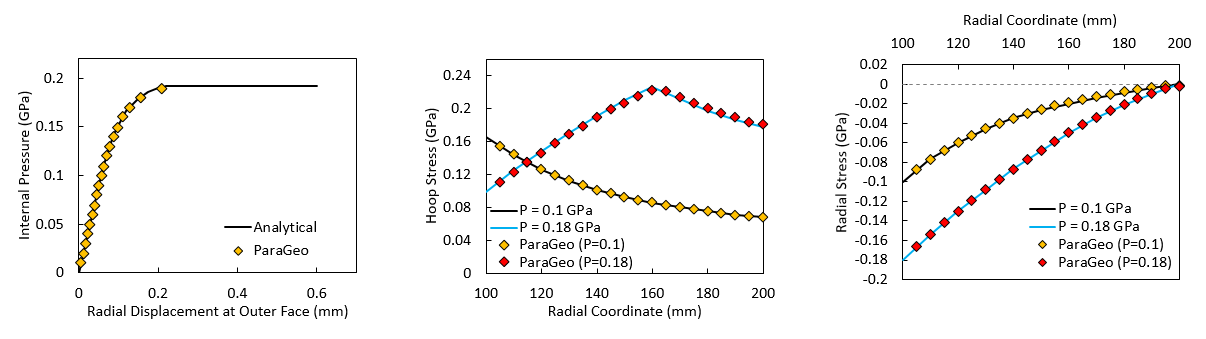
In the plots below the solution obtained from ParaGeo is compared to the analytical solution provided in de Souza-Neto et al. (2008).

The first plot on the left shows the radial displacement in the outer surface of the cylinder as a function of the applied internal pressure. As can be seen ParaGeo solution is in good agreement with the analytical one which shows an initial linear elastic behaviour for internal pressures of 0 to c.a. 0.1 GPa and starts to behave in a non-linear manner for larger pressures. It can be seen that the analytical function shows a maximum internal pressure that can be achieved which can no be exceeded. This corresponds to the collapse pressure that occurs when the plastic front reaches the outer surface (the entire cylinder becomes plastified) with continuously increasing displacements at constant pressure. De Souza-Neto et al. (2008) estimated that collapse pressure corresponds to 0.19209 GPa for the current problem. As can be seen with the current set up an approximation of such collapse pressure has been obtained at step 19 (pressure of 0.19 GPa) with the subsequent steps not converging (as the solution is not unique for pressures larger than the collapse pressure).

The two plots on the center and on the right show the hoop and radial stress distribution along the cylinder radius for applied internal pressures of 0.1 GPa and 0.18 GPa respectively. As can be seen ParaGeo solutions are also in good agreement with the analytical solutions. As can be seen for an internal pressure of 0.1 GPa the maximum hoop stress is located at the internal face, because plastic strains have still not developed. For larger pressures plastic strains develop starting at the inner surface and the plastic front moves towards the outer surface as internal pressure increases (see that the maximum hoop stress for an internal pressure of 0.18 is at a radial coordinate of c.a. 160 mm). Note that the maximum hoop stress is located next to the plastic strain front. The radial stress is maximum at the internal surface where it is equal to the internal pressure and decreases to zero towards the outer surface.

Imp_001_Case01_02

Comparison of analytical solution provided by de Souza Neto et al. (2008) and ParaGeo results for stresses and displacements.

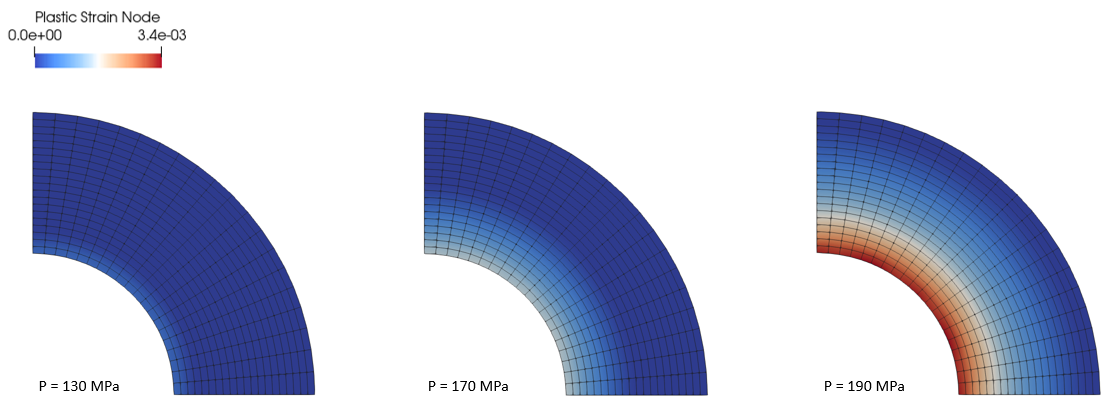
In the plots below plastic strain distribution for three internal pressures is shown. As can be seen the plastic strain front moves from the internal surface at early times to the outer surface as internal pressure increases.

Imp_001_Case01_03

Evolution of plastic strain distribution as internal pressure increases.

Case01b

An additional case Case01b is set to demonstrate the effect of the implicit solver-related keywords setup on the convergence results and steps performed. The data set up is shown below.

Data File

* Control_data

! ============================================

Control_title "init"

Solution_algorithm 7

Initial_time_increment 0.1

Minimum_time_increment 0.05

Maximum_time_increment 0.11

Maximum_number_time_steps 30

Target_number_iterations 3

Maximum_number_iterations 12

Displacement_norm_tolerance 0.01

Residual_norm_tolerance 0.01

Termination_time 1.0

Output_frequency_plotfile 1

Screen_message_frequency 1

1.The present example is set with a low Target_number_iterations (set to 3). This is expected to cause a decrease in time increment at times where plastic strains develop as we know from previous cases that for those steps more than 3 iterations are required. This combined with a Minimum_time_increment set to 0.05 is likely to cause a premature termination of the simulation.

The summary of results for steps and convergence is shown below. For the present case the simulation is terminated after step 8 because the time increment attempts to decrease below the minimum allowed value set via Minimum_time_increment.

Step num.	Time Increment	End Time	P (GPa)	Num. Iterations	Disp. Norm	Res. Norm
1	0.1	0.1	0.02	2	0.00	0.00
2	0.1	0.2	0.04	2	0.00	0.00
3	0.11	0.31	0.062	2	0.00	0.00
4	0.11	0.42	0.084	2	0.00	0.00
5	0.11	0.53	0.106	2	0.00	0.00
6	0.11	0.64	0.128	5	0.116E-3	0.00
7	0.76931E-1	0.71693	0.143386	5	0.459E-2	0.00
8	0.53803E-1	0.77073	0.154146	4	0.593E-2	0.00

Summary of step and convergence results for Case01b

References

Eduardo A. de Souza Neto, Djordje Peric and David R. J. Owen. Computational methods for plasticity: Theory and aplications. (Wiley, Chichester, 2008), pp. 244-247