Case02 Boundary Optimisation Using the Super Element
The present case is identical to Case01 except that the super element approach is used in the optimisation procedure. Hence it is recommended to be familiar with Case01 and have undertaken the SuEl_001 tutorial example beforehand.
When using the super element in the optimization procedure the set up of the .inp file and folder structure is mostly identical with the only differences being:
1.The super element must be created before running the optimisation procedure
2.The template data file must include Super_element_control data structure set to use the super element
The data for the present case is provided in MEM_003\Case02\Data. For the present case the folder structure includes an additional folder in MEM_003 \Case02\Data\Create SE where the super element is created.
Super Element Creation
The creation of the super element for usage in the optimisation procedure follows a two step process that requires to run the files MEM_003_Case02_Create.dat and then MEM_003_Case02_Use.dat
MEM_003_Case02_Create.dat
After running MEM_003_Case02_Create.dat the file MEM_003_Case2.suelmat will be output. Then in the next step of super element preparation this file will be updated.
MEM_003_Case02_Use.dat
After running the file MEM_003_Case02_Use.dat the file MEM_003_Case02.suelmat is updated and the file MEM_003_Case02.neinods is output. Those files will be required to run the optimisation procedure.
|
Template: Data File Description
The template data file MEM_003_Case02.dat file is identical to Case01 template data file except that it includes Super_element_control data set to Use the super element. In fact the data file is identical to the MEM_003_Case02_Use.dat file in MEM_003\Case02\Data\Create_SE but with the difference that the Parameterised_boundary data is left in blank (as the data will be populated with different displacement values for each model generated by ParaGeoInv).
Super Element Data
Parameterised_boundary
The Parameterised_boundary data structure is defined in blank. The data defining the displacement magnitude will be populated by ParaGeoInv during the inversion analysis.
|
Results
The results for the project are in MEM_003\Case02\Results. In MEM_003\Case02\Results\Test there are results for the file named MEM_003_Case02_186Reflate.dat which is a case manually run with plot file output and reflate results from the optimal model.
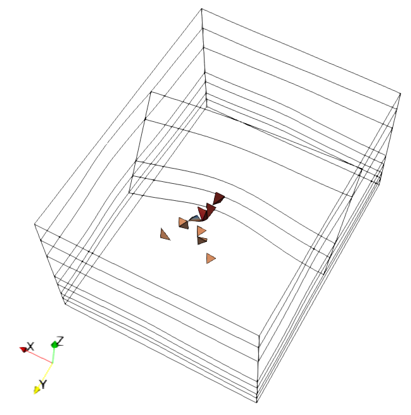
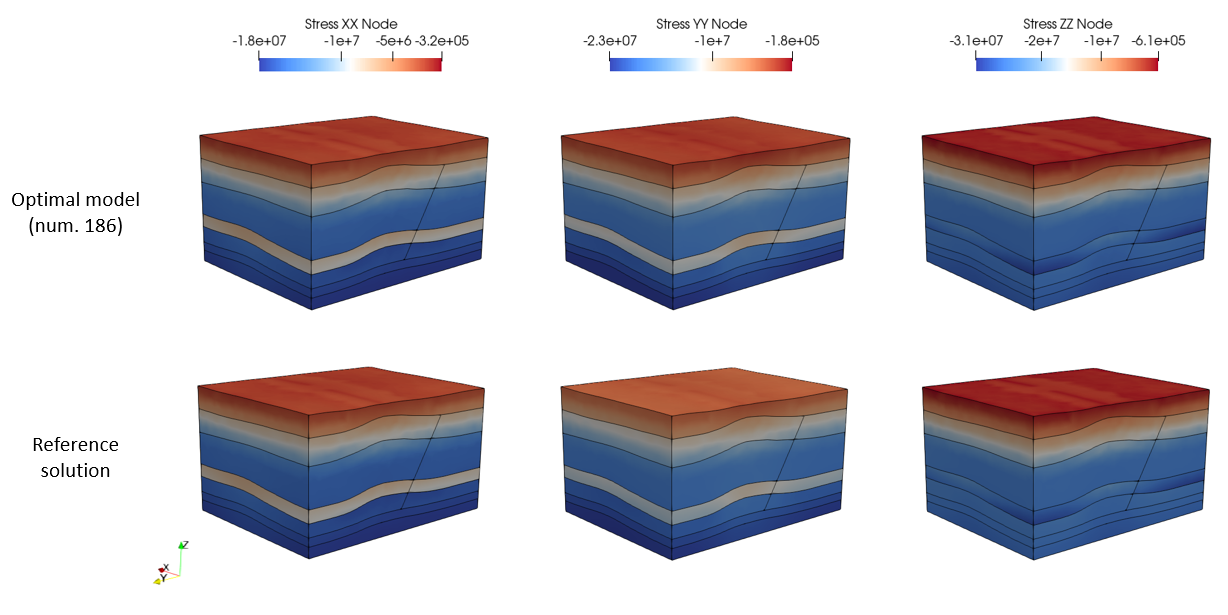
For the present case the iterative algorithm has converged to a value of 24.1 m for the displacement applied to the North boundary although it has not satisfied the convergence criteria imposed, finishing with a Misfit value of 0.1901E-01 (c.a. 2%). Note that the displacement derived from the inverse analysis (24.1 m) has a 3.6% of error relative to the one used to generate the target solution (25.0 m). Nonetheless in the figures below it can be seen that the stress distributions are very similar to the target solution. Also below is provided a figure that shows the retained elements (from the retained history point sets). Note that such figure may be obtained from the plot file from the "Use" stage (as opposed to the "Reflate") by applying a Threshold filter based on a stress element variable and set the maximum stress to a non-zero (negative) value.
Retained elements (from the retained history point sets).
Comparison of stress distributions for the optimal model from the present case and the reference solution.
Standard Simulation vs Super Element Approach
The present case has shown how to use the Super Element (SE) approach within the boundary optimization MEM workflow. The SE is advantageous in that it helps to save computational times when numerous simulations of the same model setup are needed to be performed. For the present case however it runs relatively quickly even using the standard simulation as the model has relatively small number of nodes and elements (9279 and 46488 respectively). Thus with the aim of demonstrating the benefits of the SE approach in terms of CPU time savings a finer mesh version of the current model has been run (both standard simulation and with the super element approach).
The finer mesh version of the model has c.a. 898,000 nodes and c.a. 5,365,000 elements. Although many MEMs may have meshes with many more elements and nodes than that (of the order of 1 order of magnitude more elements) this setup is enough to demonstrate CPU time savings. In addition it has to be noted that when using the implicit solver RAM memory may be a technical-limiting factor as it is easy to run out of memory for models with a large number of elements. Thus it is generally recommended to perform the optimisation procedure with a coarser mesh version of the model of interest as the differences of the optimised displacement are expected to be rather small compared to the original model. The CPU times associated to the simulations are provided in the table below.
CPU times obtained from different runs with and without the super element approach
As can be derived from the table above the SE approach in such case provides a clear benefit in CPU time saving with a speed up factor on the simulation time of 256. As can be seen the CPU time spent on creating the Super Element is similar to the time spent on two standard simulations. Hence the benefit of applying the SE approach is gained even after the first sample of models run during the optimisation procedure (as more than two models per sample are expected). To have an idea on the time savings lets consider an inversion analysis that would require 20 samples of 6 models each to converge to an optimised displacement. The standard approach will accumulate a total CPU time of 4.4 days whereas the Super Element approach would only require 2.3 hours.
|