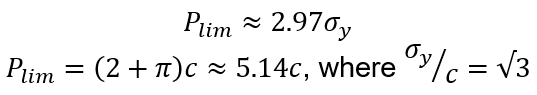Val_004b Strip Footing Collapse
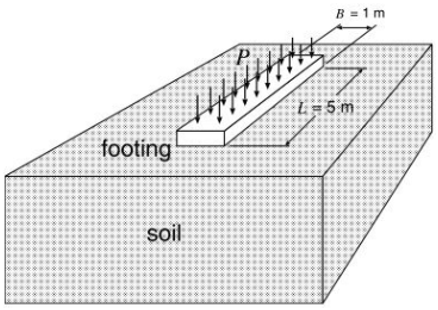
Problem Description
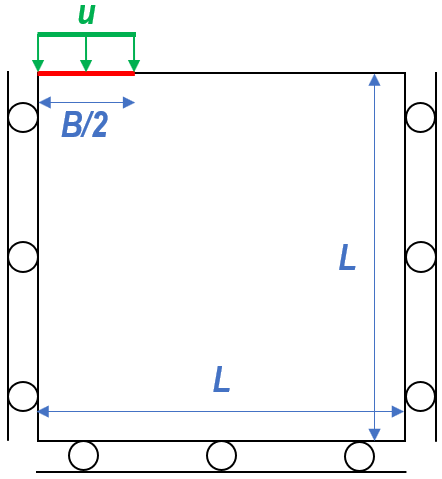
A strip footing lying on soil (assumed to be infinite medium) is subjected to vertical pressure through prescribed displacement u until the bearing capacity of the footing Plim is reached. This limit load is predicted using von-Mises elastoplasticity model. A plot of normalised pressure vs. normalised settlement is to be plotted. The simulation model is constrained with symmetry boundary conditions on the right, left and bottom boundaries. Part of the boundary with length B/2 is prescribed with downward displacement of 2m, as illustrated below.
The theoretical limit load for this problem was derived by Hill, expressed by
|
Mesh Discretisation
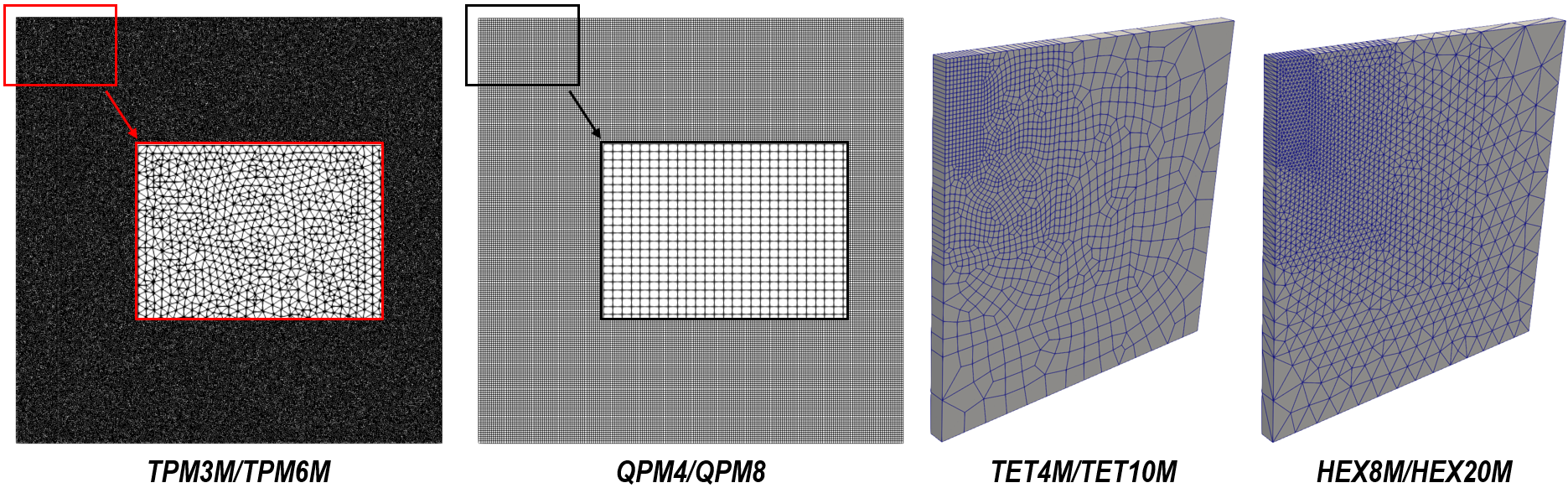
Fifteen element types have been used in this test case, with 12 element types for implicit analysis and 3 types for explicit analysis. It is noted that the standard linear triangular and tetrahedral-based elements are not recommended for this test case. The followings illustrate some examples of meshed models that have been used in 2D and 3D cases. The purpose of using fine-sized triangular and quadrilateral meshes is to plot more distinct plastic strain contour in the final results. If users only seek to predict the limit load of the model, coarser mesh would have served this purpose well.
Example of meshed models for 2D and 3D cases
|
Data File Descriptions
The data files for the different element types are in Val_004\strip_footing. The different cases are in different sub-folders according to the dimensions (2D/3D), solver (explicit/implicit) and element type used for each specific case.
The basic data includes: 1Geometry_data imports geometry file for 3D cases in *.geo format that has been created using Gmsh and made compatible using ParaGeo pre-processing procedures. In 2D cases, the geometry is created directly through data file without the aforementioned pre-processing. 2Geometry_set groups multiple geometry entities under convenient geometry set names. 3Group_control_data activates geomechanical field for the current simulation group. 4Group_data sets the group name, element type, material name, porous flow type and the associated volume entity. 5Material_data defines the material properties of the model. 6Support_data constrains the displacement freedom on each surface accordingly. 7Global_loads defines the prescribed displacement loading on the geometry set associated with the vertical pressure of the strip footing. 8Damping_global_data sets a global damping ratio of 2%. 9Control_data defines the solution algorithm (e.g. 1 for explicit transient dynamic algorithm, 7 for nonlinear implicit algorithm), termination time, etc.
Only key data structures are shown below.
Group_data
Material_data
Global_loads
|
Results
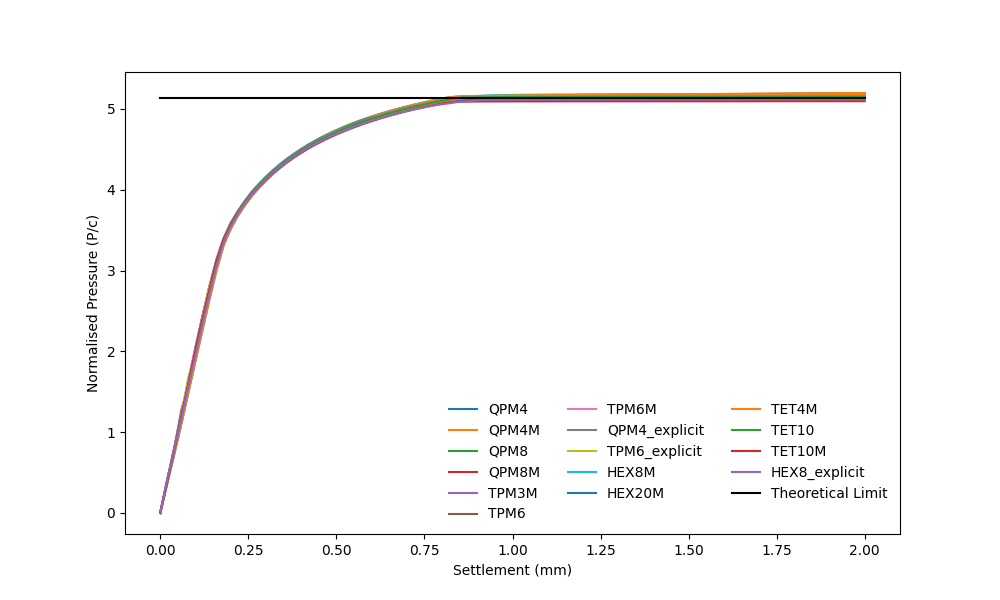
Overall, the simulation results converge to the theoretical limit load. The plots almost overlap each other from the initial loading stage towards the limit load. Slight hardening has been implemented in order to visualise the collapse on the plot, i.e., significant increase in settlement driven by a small increment in the applied pressure. The prediction difference among the tested elements is only augmented towards the limit load. The plateau corresponds to the theoretical limit load ratio (Plim/c ≈ 5.14).
Load-displacement curve for strip-footing collapse problem. Comparison of numerical solutions derived from different elements with theoretical limit for both 2D and 3D cases.
The following figures show the results of strip-footing model. Plastic strain and effective mean stress are plotted at the final time step. As the load increases, strain localisation gradually develops to form a pattern resembling curvilinear line, which is consistent with the slip-line field solution by Hill. These elements also demonstrate consistent results in terms of effective mean stress, particularly in the vicinity of the loading area.
Plastic strain contour on selected element types
Effective mean stress contour on selected element types
|
References
[1] Hill, R. (1989). The Mathematical Theory of Plasticity (pp. 106, 254). New York: Oxford University Press. [2] Neto., E., Peric, D., & Owen, D. (2013). Computational Methods for Plasticity. Hoboken, N.J.: Wiley.
|